当前位置:网站首页>[mathematical modeling] - analytic hierarchy process (AHP)
[mathematical modeling] - analytic hierarchy process (AHP)
2022-04-23 18:34:00 【Xuanche_】

Analytic hierarchy process
The analytic hierarchy process (AHP)
One of the most basic algorithms in modeling competition , It is mainly used to solve evaluation problems
Solve evaluation problems , First of all, we should think of the following three questions :
- What is the goal of our evaluation ?
- What options do we have to achieve this goal ?
- What are the evaluation criteria or indicators ?( We judge good and bad by what )
Judgment matrix
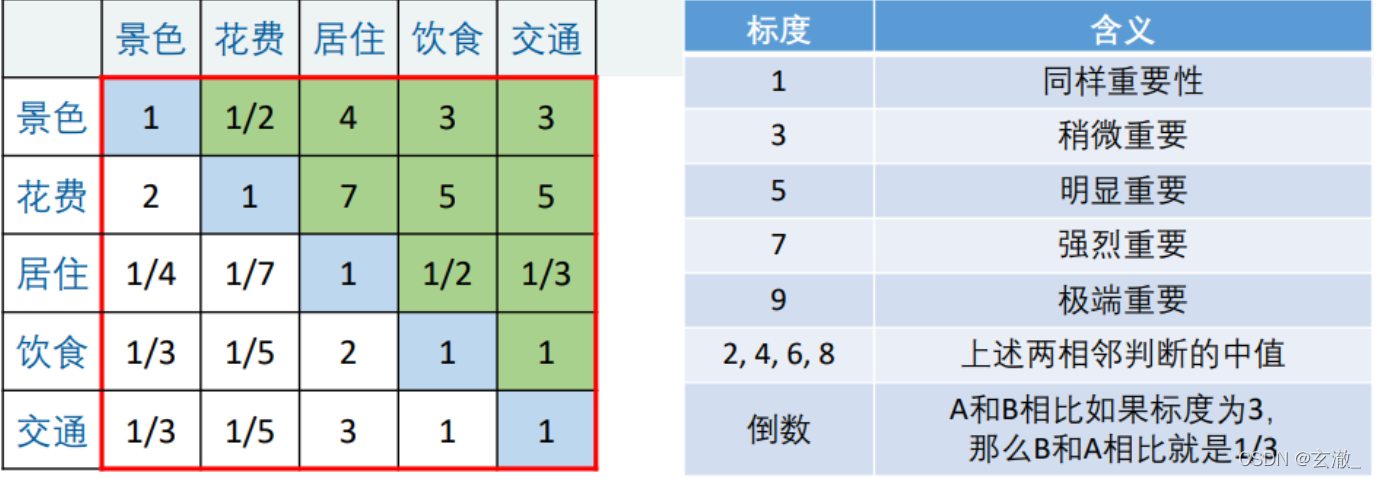
summary : This one is 5 × 5 Matrix , We remember that A, The corresponding element is a i j {a}_{ij} aij
- a i j {a}_{ij} aij The meaning of expression is , And indicators j comparison , i The importance of
- When i = j when , The two indicators are the same , Therefore, it is equally important to remember as 1, This explains that the main diagonal element is 1
- a i j {a}_{ij} aij > 0 And meet a i j {a}_{ij} aij × a j i {a}_{ji} aji = 1( We call a matrix satisfying this condition a positive reciprocal matrix )
actually , The above matrix is in the analytic hierarchy process ** Judgment matrix **
Uniform matrix
Every element in the matrix a i j {a}_{ij} aij > 0 And meet a i j {a}_{ij} aij × a j i {a}_{ji} aji = 1 , Then we call the matrix Positive reciprocal matrix .
In analytic hierarchy process , The judgment matrices we construct are positive reciprocal matrices .
If the positive reciprocal matrix satisfies a i j {a}_{ij} aij × a j k {a}_{jk} ajk = a i k {a}_{ik} aik, Then we call it a uniform matrix .
Consistency check

lemma :A by n Square matrix , And r(A) = 1, be A There is an eigenvalue tr(A), Other eigenvalues are 0
therefore , The rows of the consistency matrix are proportional , So the eigenvalue of the uniform matrix is 1
According to lemma : The uniform matrix has an eigenvalue of n, The other eigenvalues are 0

If positive reciprocal matrix ( Judgment matrix ) Satisfy a i j {a}_{ij} aij × a j k {a}_{jk} ajk = a i k {a}_{ik} aik, Then we call it a uniform matrix
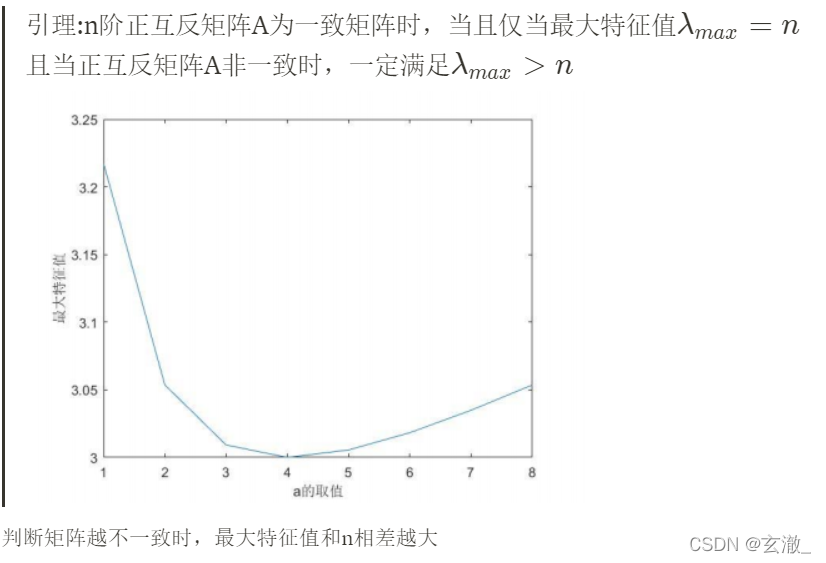
lemma :n Order positive reciprocal matrix A When it is a consistent matrix , If and only if the maximum eigenvalue λ m a x = n {\lambda}_{max} = n λmax=n
And when the positive reciprocal matrix A When inconsistent , Must be satisfied with λ m a x > n {\lambda}_{max}>n λmax>n
The more inconsistent the judgment matrix , Maximum eigenvalues and n The bigger the difference
Steps of consistency inspection
First step : Calculate the consistency index CI
C I = λ m a x − n n − 1 CI\, =\, \frac { {\lambda}_{max}\, -\, n} {n\, -\, 1} CI=n−1λmax−n
The second step : Find the corresponding average random consistency index RI

The third step : Calculate the consistency ratio CR
C R = C I R I CR=\frac {CI} {RI} CR=RICI
If CR < 0.1 , Then it can be considered that the consistency of the judgment matrix is acceptable ; Otherwise, the matrix needs to be modified

Method 1: Calculate the weight by arithmetic average
First step : Normalize the judgment matrix according to columns ( Each element is divided by its column )
The second step : Add the normalized columns ( Sum up by line )
The third step : Divide each element of the vector obtained by adding by n You can get the weight vector

Calculate the weight by geometric average method
First step : take A The elements of are multiplied by rows to get a new column vector
The second step : Open each component of the new vector n Power
The third step : The weight vector can be obtained by further normalizing the column vector

Analytic hierarchy process
Analytic hierarchy process (The Analytic Hierarchy Process namely AHP) By American operations research scientists 、 Professor at the University of Pittsburgh T . L. Saaty On 20 century 70 A comprehensive system of system analysis and decision-making founded in the s Evaluation method , It is put forward on the basis of fully studying the process of human thinking , It reasonably solves It determines the quantitative processing process of qualitative problems .
AHP The main feature is through the establishment of hierarchical structure , Translate human judgment into a number of factors On the comparison of the importance between two elements , Thus, the qualitative judgment that is difficult to quantify is transformed into an operable re To compare the above . in many instances , Decision makers can directly use AHP To make decisions , great Effectively improve the effectiveness of decision-making 、 Reliability and feasibility , But its essence is a way of thinking , It is the Complex problems are decomposed into multiple components , These factors are formed into hierarchical levels according to the dominant relationship structure , The total ranking of the relative importance of decision-making schemes is determined by pairwise comparison . Whole process body It shows the basic characteristics of human decision-making thinking , That is, decomposition 、 Judge 、 comprehensive , Overcome other ways to avoid The subjective judgment of decision makers
Solve evaluation problems , You should first think of the following three questions :
① What is the goal of our evaluation
② What options do we have to achieve this goal ?
③ What are the criteria or indicators of price ?( We judge good and bad by what )
The first step of analytic hierarchy process
Analyze the relationship between various factors in the system , Establish the hierarchical structure of the system .
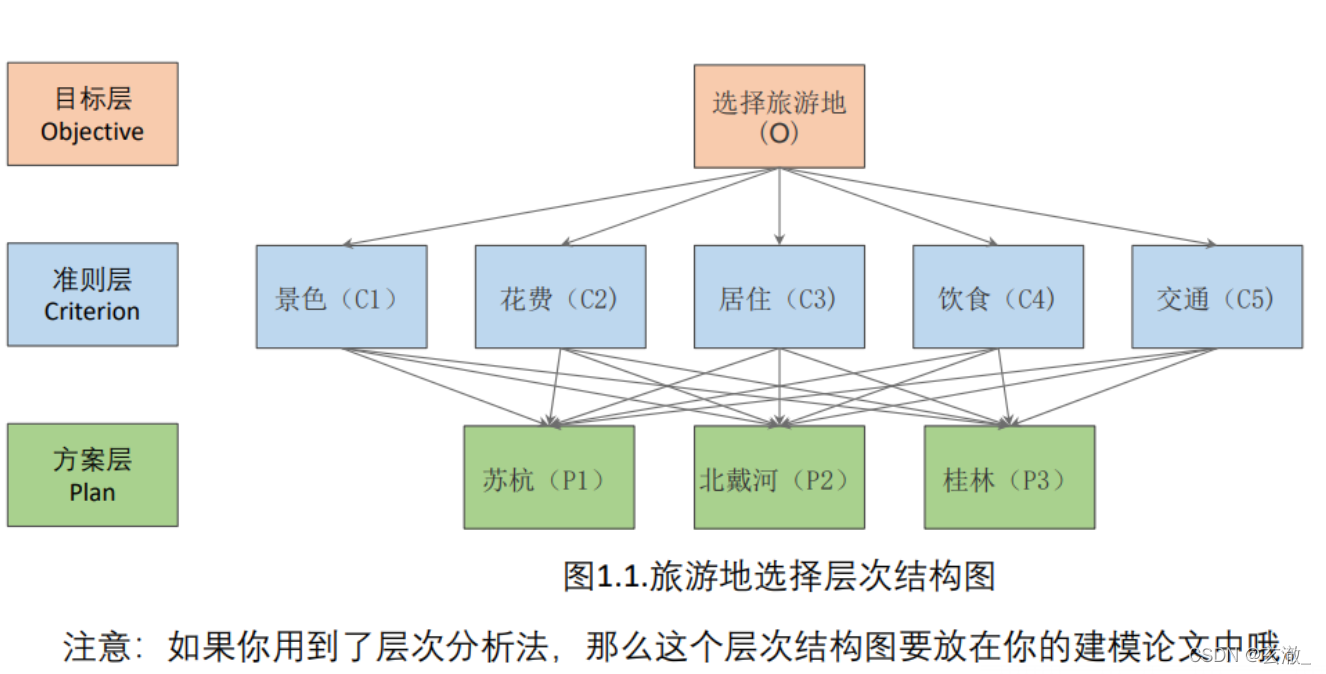
The second step of analytic hierarchy process
For the elements of the same level, the importance of a certain criterion in the previous level Compare sex in pairs , Construct pairwise comparison matrix ( Judgment matrix )
Construct judgment matrix
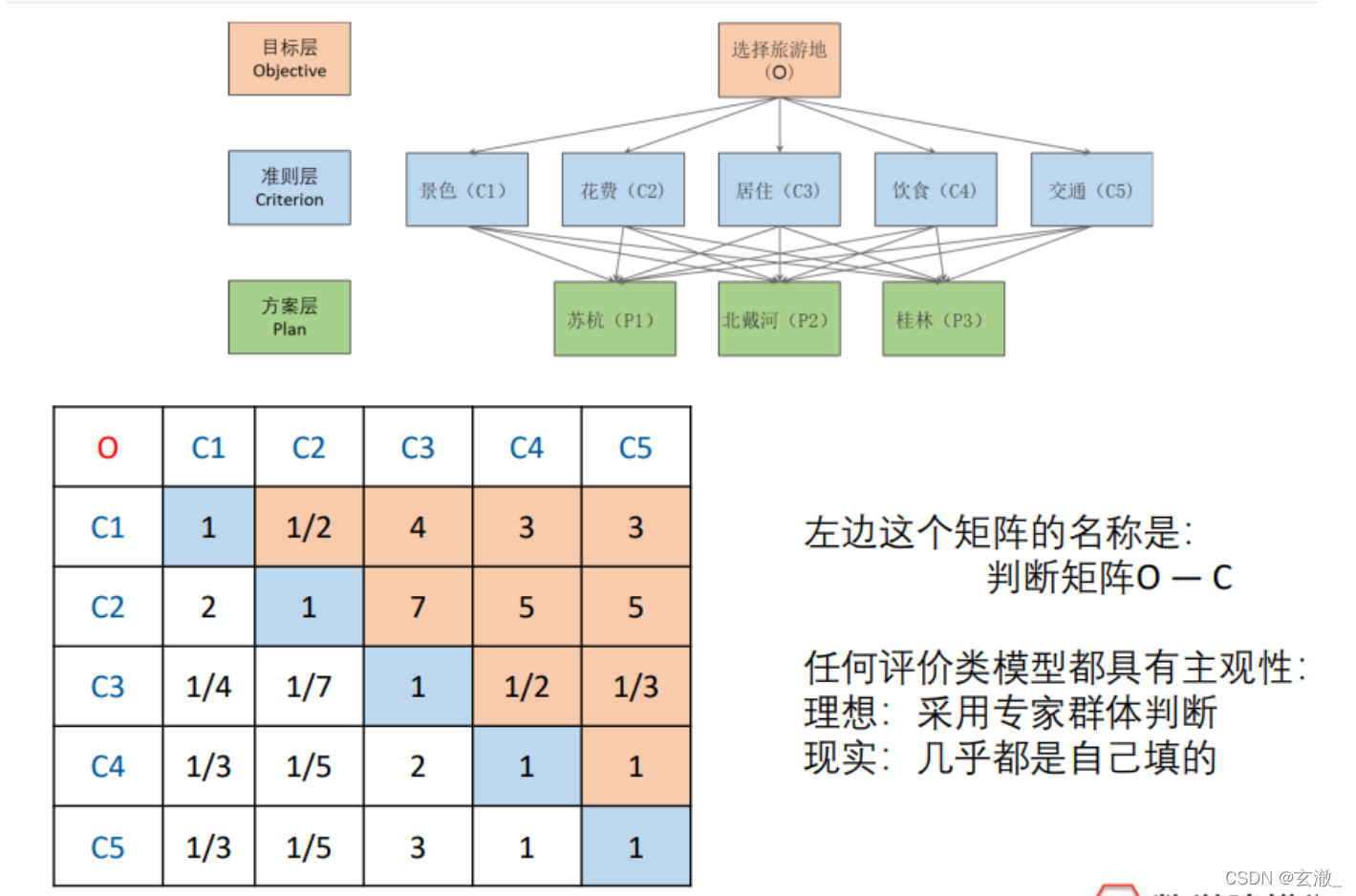
The third step of analytic hierarchy process
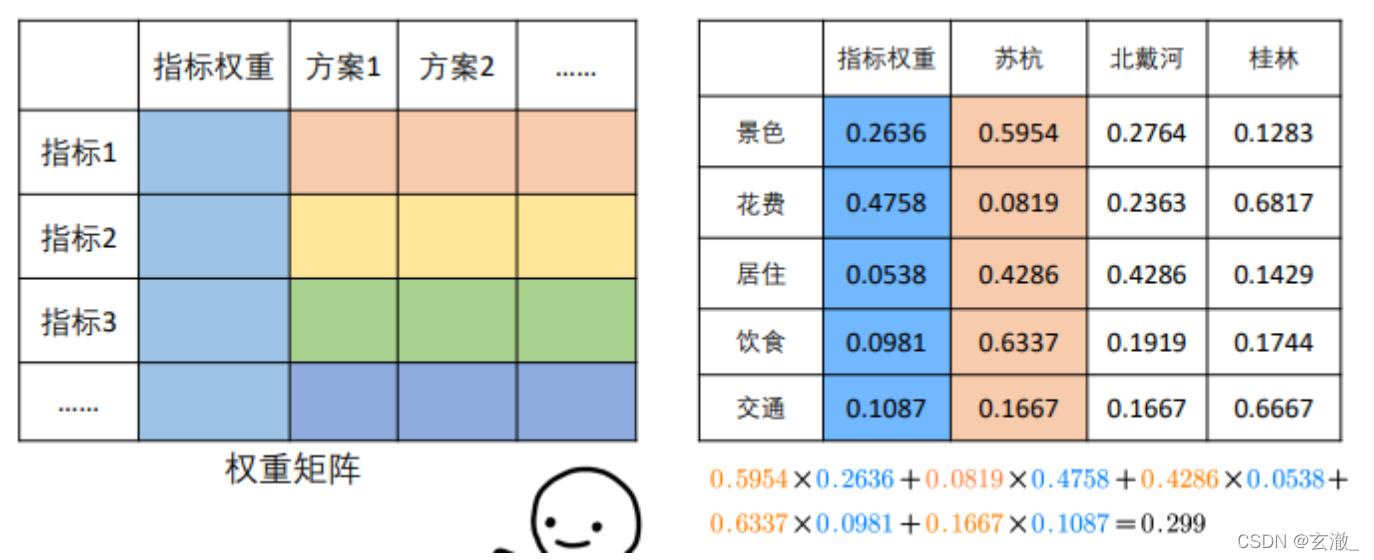
The relative weight of the compared element to the criterion is calculated from the judgment matrix , And conduct consistency inspection ( The weight can only be used after passing the test ).
There are three methods to calculate the weight
- Arithmetic average
- The geometric average method
- Eigenvalue method
We strongly recommend that you use all three methods in the competition
Previous papers used analytic hierarchy process to solve practical problems , They all use one of these methods Weight calculation , Different calculation methods may lead to deviation of results . In order to ensure the accuracy of the results robustness , In this paper, three methods are used to calculate the average value after calculating the weight respectively , Then according to Calculate the score of each scheme according to the weight matrix , And sorting and comprehensive analysis , This avoids Deviations from a single method , The conclusion will be more comprehensive 、 More effective
notes :(1) The consistency matrix does not need to be checked for consistency , Only the judgment matrix of non-uniform matrix needs to enter Line consistency check ;(2) In thesis writing , Consistency check should be carried out first , Calculate after passing the inspection The weight , What is explained in the video is just to adapt to the calculation process .
The fourth step of analytic hierarchy process
Calculate the score according to the weight matrix , And sort .
Some limitations of analytic hierarchy process
(1) The decision-making level of evaluation should not be too much , Too many words n Will be a big , Difference between judgment matrix and consistency matrix It could be big .

(2) If the data of indicators in the decision-making level is known , So how can we use these data to make The evaluation is more accurate ?
版权声明
本文为[Xuanche_]所创,转载请带上原文链接,感谢
https://yzsam.com/2022/04/202204231824246340.html
边栏推荐
- Daily CISSP certification common mistakes (April 15, 2022)
- ESP32 LVGL8. 1 - anim animation (anim 16)
- Ucosiii transplantation and use, reference punctual atom
- CISSP certified daily knowledge points (April 12, 2022)
- 串口调试工具cutecom和minicom
- According to the result set queried by SQL statement, it is encapsulated as JSON
- 【ACM】509. Fibonacci number (DP Trilogy)
- Daily CISSP certification common mistakes (April 14, 2022)
- C language simulates entering and leaving the stack, first in first out, first in first out, shared memory
- 昇腾 AI 开发者创享日全国巡回首站在西安成功举行
猜你喜欢

Robocode tutorial 3 - Robo machine analysis
How to virtualize the video frame and background is realized in a few simple steps
【ACM】376. 摆动序列
ctfshow-web362(SSTI)
Halo open source project learning (VII): caching mechanism
Function recursion and solving interesting problems

多功能工具箱微信小程序源码
Nodejs installation
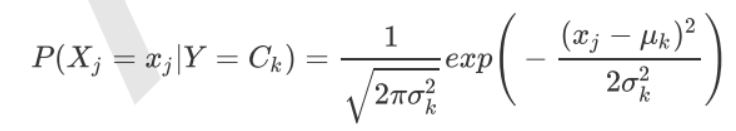
机器学习实战 -朴素贝叶斯
How to restore MySQL database after win10 system is reinstalled (mysql-8.0.26-winx64. Zip)
随机推荐
Quantexa CDI(场景决策智能)Syneo平台介绍
Daily network security certification test questions (April 14, 2022)
Robocode tutorial 3 - Robo machine analysis
QT notes on qmap container freeing memory
ESP32 LVGL8. 1 - event (event 17)
ctfshow-web362(SSTI)
Daily CISSP certification common mistakes (April 12, 2022)
SQL database syntax learning notes
Cutting permission of logrotate file
Mysqldump backup database
机器学习理论之(8):模型集成 Ensemble Learning
Ctfshow - web362 (ssti)
Connection mode of QT signal and slot connect() and the return value of emit
14 py games source code share the second bullet
使用 bitnami/postgresql-repmgr 镜像快速设置 PostgreSQL HA
ESP32 LVGL8. 1 - BTN button (BTN 15)
深入理解 Golang 中的 new 和 make 是什么, 差异在哪?
机器学习实战 -朴素贝叶斯
Daily CISSP certification common mistakes (April 11, 2022)
With the use of qchart, the final UI interface can be realized. The control of qweight can be added and promoted to a user-defined class. Only the class needs to be promoted to realize the coordinate