Pytorch: the pit between train mode and eval mode

Preface

   The blogger was accidentally in the recent development process pytorch in train Patterns and eval It's a pit o(*≧д≦)o!!, Let's not say the cause of the pit , This article will introduce in detail train Patterns and eval The impact of pattern misuse on the model and BatchNorm The mathematical principle of .

1. train Patterns and eval Pattern

   Have used pytorch The partners of the deep learning framework must know , Usually we add... Before training the model model.train() This line of code , Or not at all , And before testing the model model.test() This line of code .
   Let's take a look at what these two modes do ：

    def train(self: T, mode: bool = True) -> T:
        r"""Sets the module in training mode. This has any effect only on certain modules. See documentations of particular modules for details of their behaviors in training/evaluation mode, if they are affected, e.g. :class:`Dropout`, :class:`BatchNorm`, etc. Args: mode (bool): whether to set training mode (``True``) or evaluation mode (``False``). Default: ``True``. Returns: Module: self """
        if not isinstance(mode, bool):
            raise ValueError("training mode is expected to be boolean")
        self.training = mode
        for module in self.children():
            module.train(mode)
        return self

    def eval(self: T) -> T:
        r"""Sets the module in evaluation mode. This has any effect only on certain modules. See documentations of particular modules for details of their behaviors in training/evaluation mode, if they are affected, e.g. :class:`Dropout`, :class:`BatchNorm`, etc. This is equivalent with :meth:`self.train(False) <torch.nn.Module.train>`. See :ref:`locally-disable-grad-doc` for a comparison between `.eval()` and several similar mechanisms that may be confused with it. Returns: Module: self """
        return self.train(False)

   According to the above Official source code , You can get the following information ：

eval()	 take  module  Set to test mode ,  It will affect some modules ,  such as Dropout and BatchNorm,  And  self.train(False)  equivalent 
train(mode=True)	 take  module  Set to training mode ,  It will affect some modules ,  such as Dropout and BatchNorm

  Dropout and BatchNorm The reasons for being favored are as follows ：

# Dropout
self.dropout = nn.Dropout(p=0.5)

  Dropout The layer can then reduce the connections of neurons , It can turn a dense neural network into a sparse neural network , This can alleviate over fitting ( The more neurons are connected in neural networks , The more complex the model , The more easily the model fits )( in fact ,Dropout Layer performance is not so good ).

# BatchNorm2d
self.bn = nn.BatchNorm2d(num_features=128)

  BatchNorm Layers can be used to mini-batch Data are normalized to accelerate neural network training , Accelerate the convergence speed and stability of the model , besides , It can also alleviate the gradient explosion problem caused by too many layers of the model .

   In training the model , Set the mode of the model to train It's easy to understand , But when we test the model , We need to use all the neurons of the neural network , At this time, it is necessary to prohibit Dropout Layers are working , Otherwise , The accuracy of the model will be reduced . And in test mode BatchNorm The layer will use the training mean and variance , The mean and variance of the input data when the test model is no longer used ( Explain later why ).

  OK, With the above brief introduction , Let's do a little experiment , Take a look at train Patterns and eval How much does the pattern affect the results of the model . By default , After building the model, you are in train Pattern ：

from torchvision.models import resnet152


if __name__ == '__main__':
    model = resnet152()
    print(model.training)

# True

   If we were testing the model , The model is not set to eval What happens in mode ？ I started from ImageNet In the data set 20 Picture to test the model ：

   Let's first look at the normal results ：

import torch
from torchvision.models import resnet152
from torch.nn import functional as F
from torchvision import transforms
from PIL import Image
import pickle
import glob
import pandas as pd


if __name__ == '__main__':
    label_info = pd.read_csv('imagenet2012_label.csv')

    transform = transforms.Compose([
        # transforms.Resize(256),
        # transforms.CenterCrop(224),
        transforms.ToTensor(),
        transforms.Normalize(
            mean=[0.485, 0.456, 0.406],
            std=[0.229, 0.224, 0.225]
        )])

    model = resnet152()
    ckpt = torch.load('pretrained/resnet152-394f9c45.pth')
    model.load_state_dict(ckpt)
    model.eval()
    # model.train()

    file_list = glob.glob('imgs/*.JPEG')
    file_list = sorted(file_list)
    for file in file_list:
        img = Image.open(file)

        img = transform(img)
        img = img.unsqueeze(dim=0)

        output = model(img)
        data_softmax = F.softmax(output, dim=1).squeeze(dim=0).detach().numpy()
        index = data_softmax.argmax()

        results = label_info.loc[index, ['index', 'label', 'zh_label']].array
        print('index: {}, label: {}, zh_label: {}'.format(results[0], results[1], results[2]))

   The result is absolutely right ：

index: 162, label: beagle, zh_label:  Dog 
index: 101, label: tusker, zh_label:  Elephant 
index: 484, label: catamaran, zh_label:  Sailboat 
index: 638, label: maillot, zh_label:  Swimsuits 
index: 475, label: car_mirror, zh_label:  reflector 
index: 644, label: matchstick, zh_label:  A match 
index: 881, label: upright, zh_label:  The piano 
index: 21, label: kite, zh_label:  bird 
index: 987, label: corn, zh_label:  corn 
index: 141, label: redshank, zh_label:  bird 
index: 335, label: fox_squirrel, zh_label:  The squirrel 
index: 832, label: stupa, zh_label:  palace 
index: 834, label: suit, zh_label:  Suit 
index: 455, label: bottlecap, zh_label:  Bottle cap 
index: 847, label: tank, zh_label:  tanks 
index: 248, label: Eskimo_dog, zh_label:  Dog 
index: 92, label: bee_eater, zh_label:  bird 
index: 959, label: carbonara, zh_label:  pasta 
index: 884, label: vault, zh_label:  Arcade 
index: 0, label: tench, zh_label:  fish 

   Next, set the model to train Pattern , Test again , give the result as follows ：

index: 600, label: hook, zh_label:  hook 
index: 600, label: hook, zh_label:  hook 
index: 600, label: hook, zh_label:  hook 
index: 600, label: hook, zh_label:  hook 
index: 600, label: hook, zh_label:  hook 
index: 600, label: hook, zh_label:  hook 
index: 600, label: hook, zh_label:  hook 
index: 600, label: hook, zh_label:  hook 
index: 463, label: bucket, zh_label:  Buckets 
index: 600, label: hook, zh_label:  hook 
index: 463, label: bucket, zh_label:  Buckets 
index: 600, label: hook, zh_label:  hook 
index: 600, label: hook, zh_label:  hook 
index: 600, label: hook, zh_label:  hook 
index: 600, label: hook, zh_label:  hook 
index: 463, label: bucket, zh_label:  Buckets 
index: 600, label: hook, zh_label:  hook 
index: 600, label: hook, zh_label:  hook 
index: 600, label: hook, zh_label:  hook 
index: 600, label: hook, zh_label:  hook 

   Oh, Ho , What happened? ！ This result is very surprising , The model output is completely wrong ！
  ResNet152 It doesn't contain Dropout layer , There is only one reason for this result , That's it BatchNorm What the hell .

2. BatchNorm

   stay pytorch in ,BatchNorm Of Definition as follows ：

torch.nn.BatchNorm2d(num_features, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True, device=None, dtype=None)

# Parameters:
- num_features:	C from an expected input of size (N, C, H, W)
- eps: a value added to the denominator for numerical stability. Default: 1e-5
- momentum: the value used for the running_mean and running_var computation. Can be set to None for cumulative moving average (i.e. simple average). Default: 0.1
- affine: a boolean value that when set to True, this module has learnable affine parameters. Default: True
- track_running_stats: a boolean value that when set to True, this module tracks the running mean and variance, and when set to False, this module does not track such statistics, and initializes statistics buffers running_mean and running_var as None. When these buffers are None, this module always uses batch statistics. in both training and eval modes. Default: True

# Shape:
- Input: (N, C, H, W)
- Output: (N, C, H, W)(same shape as input)

# num_features  Indicates the number of input features , If input  tensor  by  (N, C, H, W),  be  num_features  The value of is  C
# eps  Represents a value added to the denominator , Prevent the occurrence of denominators of  0  The situation of , The default value is  0.00001
# momentum  In the calculation  running_mean  and  running_var  This parameter will be used when , The default value is  0.1
# affine  When set to  True  when ,BatchNorm  There are parameters to learn  γ  and  β, The default value is  True
# track_running_stats  When set to  True  when ,BatchNorm  Will track the mean and variance of the data ; When set to False when ,BatchNorm  Such statistics are not tracked , And will  running_mean  and  running_var  The statistics buffer of is initialized to  None. When these buffers are  None  when , stay  train  Patterns and  eval  In mode  BatchNorm  Always use batch Statistics ,  The default value is  True

   Build a simple model to see ：

import torch
from torch import nn


seed = 10001
torch.manual_seed(seed)


class MyModel(nn.Module):
    def __init__(self):
        super(MyModel, self).__init__()

        self.conv = nn.Conv2d(in_channels=3, out_channels=10, kernel_size=5, stride=1)
        self.bn = nn.BatchNorm2d(num_features=10, eps=1e-5, momentum=0.1, affine=True, track_running_stats=True)
        self.relu = nn.ReLU()
        self.pool = nn.AdaptiveAvgPool2d(output_size=1)
        self.linear = nn.Linear(in_features=10, out_features=1)

    def forward(self, x):
        x = self.conv(x)
        var, mean = torch.var_mean(x, dim=[0, 2, 3])
        print("x's mean: {}\nx's var: {}".format(mean.detach().numpy(), var.detach().numpy()))
        
        x = self.bn(x)
        print('-----------------------------------------------------------------------------------')
        print("x's mean: {}\nx's var: {}".format(self.bn.running_mean.numpy(), self.bn.running_var.numpy()))
        
        x = self.relu(x)
        x = self.pool(x)
        x = x.view(x.size(0), -1)
        output = self.linear(x)

        return output


if __name__ == '__main__':
    model = MyModel()

    inputs = torch.randn(size=(128, 3, 32, 32))
    model(inputs)

   Run the above model and you will find , We manually calculate the sum of mean and variance of the convoluted features BatchNorm The mean and variance calculated by the layer are not consistent , But you can find some clues , Manually calculated mean and BatchNorm The average value calculated by the layer is different 10 times , The difference is the above parameters momentum Caused by the , The default value is 0.1.

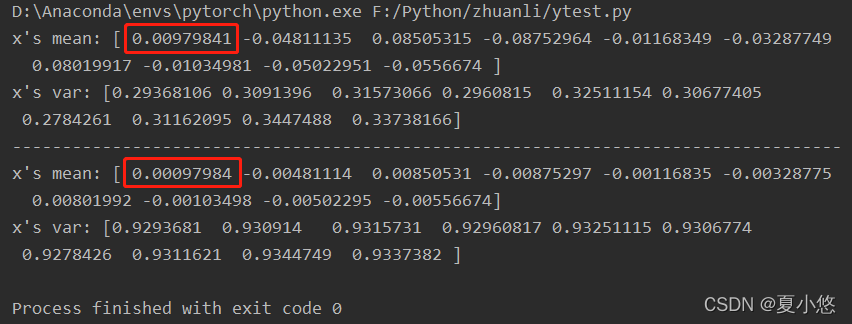
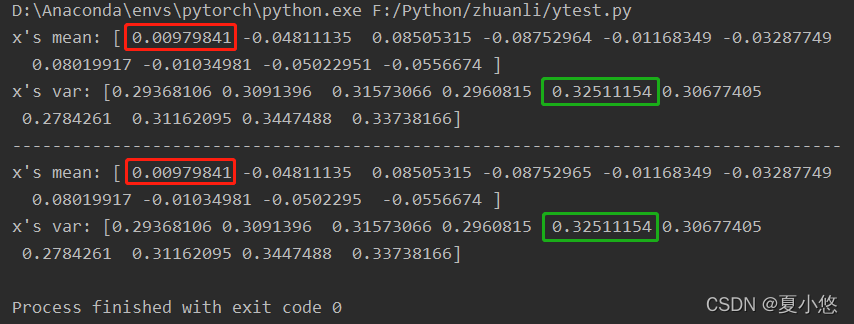
   Parameters momentum The value of is changed to 1.0, Run the model again , At this time, the sum of mean and variance of the convoluted features BatchNorm The mean and variance calculated by layer are completely consistent ：

   Let's look at the parameters affine stay BatchNorm The specific role of , The pictures below are affine=True and affine=False：

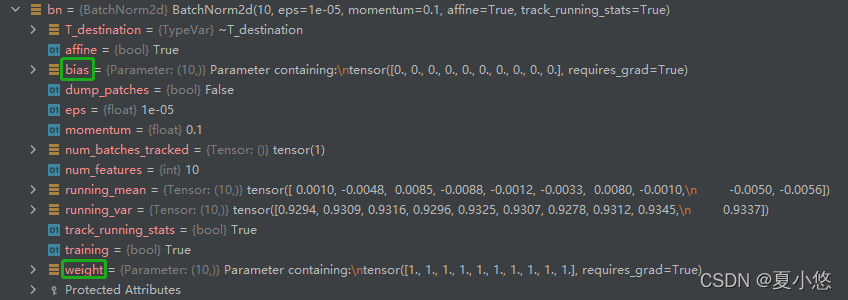
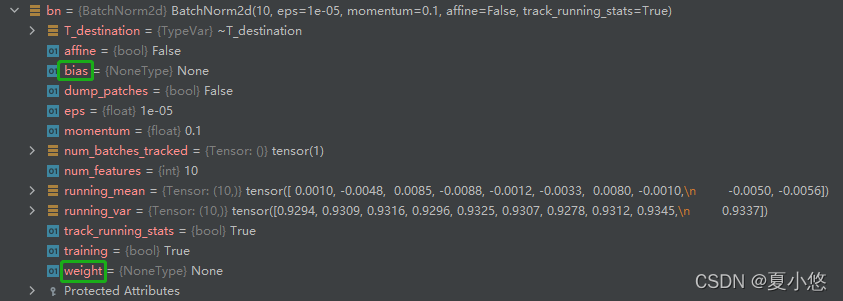
   Obviously ,affine=True when BatchNorm The layer has trainable parameters weight and bias.

   Last , Let's take another look at a very important parameter ：track_running_stats
   Look at the picture above num_batches_tracked Value , When we put the parameter track_running_stats Is set to True,BatchNorm The incoming data will be counted , At this time num_batches_tracked The value is 1, That is to record a mini-batch The average of running_mean And variance running_var. Change the code and calculate more times ：

if __name__ == '__main__':
    model = MyModel()

    inputs = torch.randn(size=(128, 3, 32, 32))
    for i in range(10):
        model(inputs)
    print('num_batches_tracked: ', model.bn.num_batches_tracked.numpy())

# num_batches_tracked: 10

   In order to be more persuasive , Let's change the code again , Let's compare BatchNorm How are the statistics ：

class MyModel(nn.Module):
    def __init__(self):
        super(MyModel, self).__init__()

        self.conv = nn.Conv2d(in_channels=3, out_channels=10, kernel_size=5, stride=1)
        self.bn = nn.BatchNorm2d(num_features=10, eps=1e-5, momentum=1.0, affine=True, track_running_stats=True)
        self.relu = nn.ReLU()
        self.pool = nn.AdaptiveAvgPool2d(output_size=1)
        self.linear = nn.Linear(in_features=10, out_features=1)

        self.var_data = []
        self.mean_data = []

    def forward(self, x):
        x = self.conv(x)

        var, mean = torch.var_mean(x, dim=[0, 2, 3])
        self.var_data.append(var)
        self.mean_data.append(mean)

        x = self.bn(x)
        x = self.relu(x)
        x = self.pool(x)
        x = x.view(x.size(0), -1)
        output = self.linear(x)

        return output


if __name__ == '__main__':
    model = MyModel()

    for i in range(10):
        inputs = torch.randn(size=(128, 3, 32, 32))
        model(inputs)

    var = model.var_data[-1]
    mean = model.mean_data[-1]
    print("x's mean: {}\nx's var: {}".format(mean.detach().numpy(), var.detach().numpy()))
    print('-----------------------------------------------------------------------------------')
    print("x's mean: {}\nx's var: {}".format(model.bn.running_mean.numpy(), model.bn.running_var.numpy()))

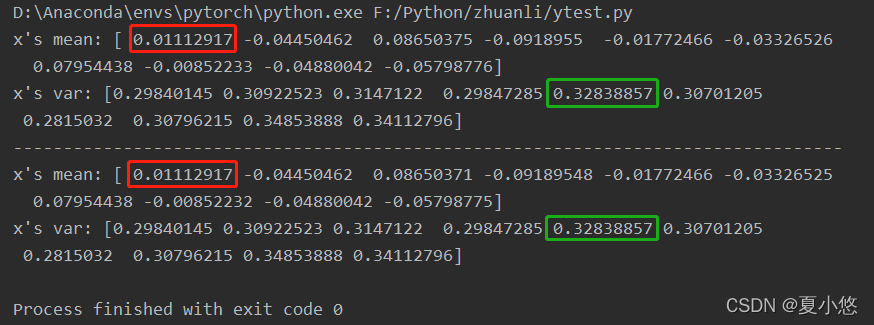
   It's not quite what I thought , I think it's the mean and variance of all samples in the past , It's not , According to the actual results ,BatchNorm The recorded mean and variance are always the last mini-batch Mean and variance of samples , That is, only the current data is normalized .

3. Principles of Mathematics

  BatchNorm The algorithm comes from Google A paper on ：Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift.

   According to the formula in the paper , You can get BatchNorm The expression of the algorithm $$\mathbf{y}=\gamma \cdot \frac{\mathbf{x}-E(\mathbf{x})}{\sqrt{Var(\mathbf{x})+ϵ}}+\beta$$   among ,$\mathbf{x}$ Is the value of the input tensor ,$ϵ$ Is a smaller floating point number , To prevent the denominator from being 0.
   With BatchNorm2d For example , The mean and variance are relative to N、H、W Three directions are calculated and averaged , As follows ：
$$E({\mathbf{x}}_c)=\frac{1}{N\times H\times W}\sum _{N,H,W}{\mathbf{x}}_c$$$$Var({\mathbf{x}}_c)=\frac{1}{N\times H\times W}\sum _{N,H,W}({\mathbf{x}}_c-E({\mathbf{x}}_c){)}^2$$   According to the calculation formula, we can know , The output of the statistic is a size of C Vector .

   Because the process of calculating statistics includes mini-batch N The average of , therefore BatchNorm Also known as batch normalization method , Just change the input tensor Data distribution of , Don't change tensor The shape of the .

   Next, let's follow the formula pytorch Medium BatchNorm2d Parameters of ：
   Parameters momentum Controlling the calculation of exponential moving average $E(\mathbf{x})$ and $Var(\mathbf{x})$ Momentum at , The calculation formula is as follows ：
$${\hat{x}}_{new}=(1-\alpha )\hat{x}+\alpha {\hat{x}}_t$$   among $\alpha$ Is the value of momentum ,${\hat{x}}_t$ It is current. $E(\mathbf{x})$ or $Var(\mathbf{x})$ Calculated value ,$\hat{x}$ Is the estimated value of the exponential moving average in the previous step ,${\hat{x}}_{new}$ Is an estimate of the current exponential moving average .
   Parameters affine Determines whether to do affine transformation after normalization , That is, whether to set $\beta$ and $\gamma$ Parameters ,affine=True Express $\beta$ and $\gamma$ Is a trainable scalar parameter ,affine=False Express $\beta$ and $\gamma$ Is a fixed scalar parameter , namely $\beta =0$,$\gamma =1$.
   Parameters track_running_stats Determines whether to use exponential moving average to estimate the current statistical parameters , The default is to use , If you set track_running_stats=False, The calculated value of the current statistic is directly used ${\hat{x}}_t$ Come on $E(\mathbf{x})$ and $Var(\mathbf{x})$ Estimate .

   Affine transformation = linear transformation + translation

Conclusion

   in application , Usually will mini-batch Set it slightly larger , such as 128, 256, If the setting is too small , It may lead to drastic changes in data , It's hard for the model to converge , After all mini-batch Only a small part of the data in the data set .