Prim、Kruskal

One 、 What is a minimum spanning tree ？

1、 Make trees

For having n Connected graph with vertices , There are at least n-1 side , Then the minimal connected subgraph connecting all vertices is a spanning tree . If you add any edge to the spanning tree of a graph , It must form a loop .

 

2、 Minimum spanning tree

For connected networks , Edges are weighted , The edges of the spanning tree are also weighted , Therefore, the sum of the weights of each side of the spanning tree is called the weight of the spanning tree , The spanning tree with the smallest weight is called the minimum spanning tree .

 
Pictured ：

 

Two 、 Minimum spanning tree algorithm

1、Prim

Implementation steps

1. Divide the vertices of the graph into two sets , aggregate A={null}, Used to store the vertices in the minimum spanning tree . aggregate B={all node}, Store vertices that have not been added to the spanning tree .
2. stay B Select any vertex in the as the starting vertex , Add to set A in . And update the A To B The distance between the vertices dist[N]
3. Select the nearest vertex , Add to set A in , And update the A To B The distance between the vertices dist[N]… Until all vertices are added to A in .

 
Pictured ：

 
Code example ：

#include <iostream>
#include <vector>
using namespace std;

const int INF = 10000;        //  infinity 
const int N = 6;              //  The number of vertices of a graph 
vector<bool> visit(N, false); //  Whether the current vertex has been added to the spanning tree 
vector<int> dist(N, INF);     //  aggregate A Medium to set B The distance between the vertices in the ,
                              // A Refers to the vertices that have been added to the spanning tree ,B Are vertices that are not added to the spanning tree 
int graph[N][N] = {           //  Graphs are represented by adjacency matrices 
    {  0,   6,   1,   5,   INF,   INF},
    {  6,   0,   5,   INF,   3,   INF},
    {  1,   5,   0,   5,     6,     4},
    {  5, INF,   5,   0,   INF,     2},
    {INF,   3,   6, INF,     0,     6},
    {INF, INF,   4,   2,     6,     0},
};

//  Find the minimum spanning tree of a graph 
// beginVertex:  Starting point 
// retrun:  The weight of the minimum spanning tree 
int Prim(int beginVertex)
{
    //  Empty the set A
    for (auto i : visit) i = false;
    //  aggregate A To the assembly B The initial distance of each vertex is infinity 
    for (auto i : dist) i = INF;
    //  Add the starting vertex to the set A
    visit[beginVertex] = true;
    printf("%c ", beginVertex + 'A');

    //  to update A To B The distance between the vertices 
    for (int i = 0; i < N; i++) dist[i] = graph[beginVertex][i];

    //  Record the minimum spanning tree weight 
    int weight = 0;
    //  take B All vertices in the are added to one by one A in 
    for (int i = 1; i < N; i++) {
        //  Record the vertex with the shortest distance 
        int index;
        int min = INF;
        //  Find the nearest vertex 
        for (int j = 0; j < N; j++) {
            if (!visit[j] && dist[j] < min) {
                min = dist[j];
                index = j;
            }
        }
        //  Put the vertex index From the collection B Move to collection A
        visit[index] = true;
        weight += min;
        printf("%c ", index + 'A');

        //  to update A To B The distance between the vertices 
        for (int i = 0; i < N; i++) {
            if ( !visit[i] && dist[i] > graph[index][i])
                dist[i] = graph[index][i];
        }
    }
    cout << endl;

    return weight;
}

int main()
{
    for (int i = 0; i < N; i++)
        printf("begin: %c, weight: %d\n", i+'A', Prim(i));

    return 0;
}

result ：

A C F D B E 
begin: A, weight: 15
B E C A F D 
begin: B, weight: 15
C A F D B E 
begin: C, weight: 15
D F C A B E 
begin: D, weight: 15
E B C A F D 
begin: E, weight: 15
F D C A B E 
begin: F, weight: 15

 
Algorithm complexity

Prim The time complexity of is O(n²), Independent of the number of edges in the graph , Therefore, the algorithm is suitable for finding the minimum spanning tree of a network with dense edges .

 

2、Kruskal

Implementation steps

1. Divide the edges of the graph into two sets , aggregate A={null}, Used to store the edges in the minimum spanning tree . aggregate B={all edge}, Store edges that have not been added to the spanning tree .
2. selection B The smallest edge in the , And don't let A The edges that make up the loop , Add to set A in .
3. until N-1 Add an edge to A in .

The difficulty of realizing Kruskal algorithm is How to judge whether a new edge will form a loop with the selected edge , Here is the use of Union checking set Realize the combination of sets . Reference resources ： Minimum spanning tree algorithm 【 The illustration 】： The article takes you to understand what is Prim Algorithm and Kruskal Algorithm - RioTian (cnblogs.com)

Pictured ：

 
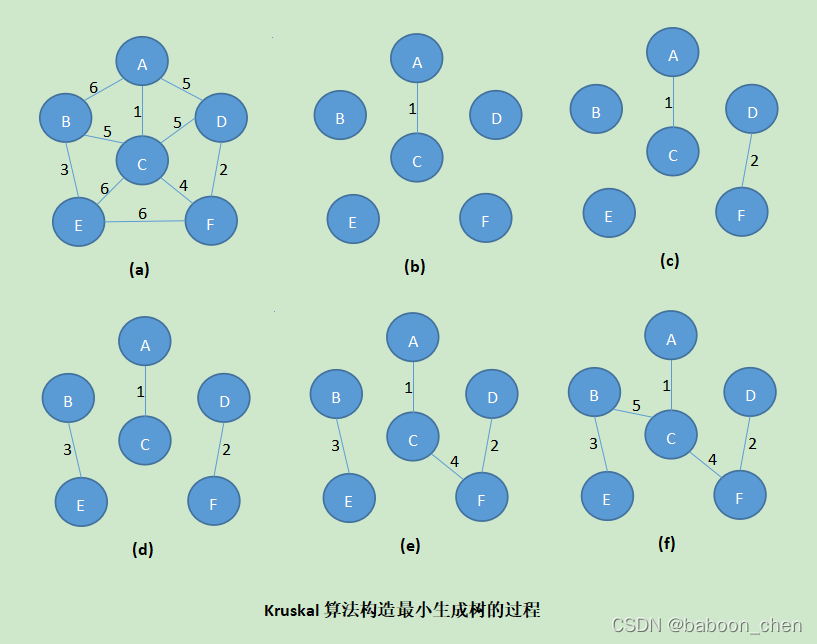
Code example ：

#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;

const int N = 10;  //  The number of sides of a graph 

struct Edge {     //  Undirected weighted edge 
    int weight;   //  A weight 
    int start;    //  The vertices A
    int end;      //  The vertices B
};
using Graph = vector<Edge>;

//  Initialize collection , Let all the points form a set , Each set contains only itself 
//  And search set initialization , The parent node of each node is itself 
int father[N] = { 0 };
//  Set size ( Influence size )
int cap[N] = { 0 };
void MakeSet()
{
    for (int i = 0; i < N; ++i) {
        father[i] = i;
        cap[i] = 1;
    }
}

//  Recursively find the parent node of the set 
//  And reset the set while looking for the parent node 
int FindSet(int x) {
    if (x != father[x])
        father[x] = FindSet(father[x]);
    return father[x];
}

// take x,y Merge into the same set 
void Union(int x, int y) {
    x = FindSet(x);
    y = FindSet(y);
    if (x == y)
        return;
    if (cap[x] < cap[y])
        father[x] = FindSet(y);
    else {
        //  Leftist thought 
        if (cap[x] == cap[y])
            cap[x]++;
        father[y] = FindSet(x);
    }
}

//  Find the minimum spanning tree of a graph 
// retrun:  The weight of the minimum spanning tree 
int Kruskal(Graph g) {
    //  The weight of the spanning tree 
    int weight = 0;

    //  Create and retrieve 
    MakeSet();

    //  from N Find... In the edge N-1 The edge with the smallest weight 
    for (int i = 0; i < N; ++i) {
        if (FindSet(g[i].start) != FindSet(g[i].end)) {
            Union(g[i].start, g[i].end);
            weight += g[i].weight;
            printf("%c->%c ", g[i].start+'A', g[i].end+'A');
        }
    }

    return weight;
}

int main() {
    Graph graph = { 
        { 6, 0, 1 },
        { 3, 1, 4 },
        { 6, 4, 5 },
        { 2, 3, 5 },
        { 5, 3, 0 },
        { 1, 0, 2 },
        { 5, 2, 1 },
        { 5, 2, 3 },
        { 6, 2, 4 },
        { 4, 2, 5 }
    };
    sort(graph.begin(), graph.end(), [](Edge a, Edge b) {return a.weight < b.weight;});
    cout << Kruskal(graph) << endl;

    return 0;
}

result ：

A->C D->F B->E C->F C->B 15

 
Algorithm complexity

Kruskal The time complexity of is O(eloge), Independent of the number of vertices in the graph , Therefore, the algorithm is suitable for finding the minimum spanning tree of a network with sparse edges .