当前位置:网站首页>进制转换间的那点事
进制转换间的那点事
2022-08-11 06:06:00 【小牛要翻身】
文章目录
前言
在学习C语言时,你是否曾被进制所支配?二进制、十进制、八进制、十六进制…明明这些数字我都认识,为什么组合在一起犹如天文数字?哈哈哈,不要怕,下面让我们一起解密进制间的那点事!
为了大家易于理解,本章就只讲解正整数之间的转化,如果想深入理解,可以去了解小数与负数之间的转换,这些大家可以适当拓展,这里就不在讲解喽。
一、常见进制数组成
1.1、二进制数组成
| 0 | 1 | 2 |
|---|
1.2、八进制数组成
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|
1.3、十进制数组成
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|
1.4、十六进制数组成
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
|---|
二、进制间转换原则
在进行进制转换时有一基本原则:转换后表达的“量”的多少不能发生改变。即等大不变原则。
就像二进制中的111个苹果和十进制中的7个苹果是一样多的。
三、N进制转换为10进制
3.1、按权相加法
位权: N进制整数转换为10进制整数采用
“按权相加”法。这里的“权”指的是位权,数制中每一固定位置对应的单位值称为位权。
详解: 对于多位数,也就是当处在某一位上的“1”所表示的数值的大小,称为该位的位权。例如十进制第一位的位权为100=1,第2位的位权为101=10,第3位的位权为102=100;而二进制第一位位权为20=1,第2位的位权为21=2,第3位的位权为22=4。
位权计算规则: 由十进制、二进制整数拓展到对于 N进制整数数,整数部分第 i位的位权为 N(i-1)
下面使用两个实例展示转换过程:
3.2、二进制转换为10进制
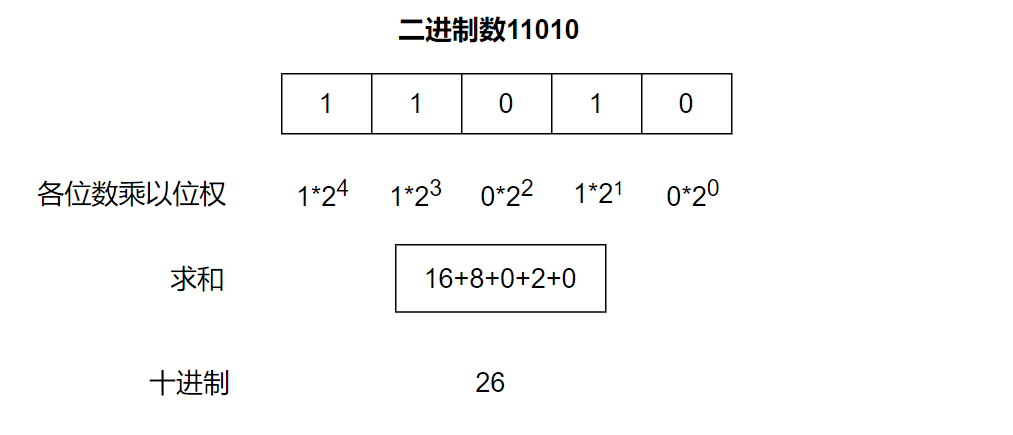
例如:二进制数11010转化为十进制数26的过程:
3.3、十六进制转化为10进制
例如:十六进制数10E1转化为十进制数4321的过程:

四、10进制转换为N进制
4.1、“除N取余,逆序排列”法
十进制整数转换为N进制整数采用
“除N取余,逆序排列”法。
具体做法是:
- 将N作为除数,用十进制整数除以N,可以得到一个商和余数;
- 保留余数,用商继续除以N,又得到一个新的商和余数;
- 仍然保留余数,用商继续除以N,还会得到一个新的商和余数……;
- 按上述步骤反复执行,直到商为零
- 最后将先得到的余数作为低位后得到的余数作为高位,如此逆序排列就可以得到转换后的N进制数
下面用2个实例向大家展示转换过程
4.2、十进制转换为2进制数
例如:十进制数42转换为2进制数101010的过程:
4.3、 十进制数转换为8进制数
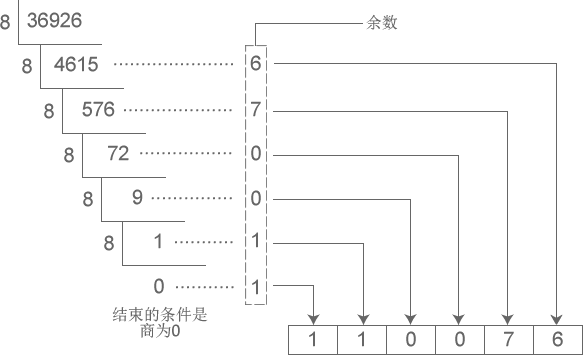
例如:十进制数36926转换为八进制数110076的过程:
五、二进制和八进制十六进制之间的那点事
5.1、二进制与八进制之间的转换
方法: 二进制整数转换为八进制整数时,每三位二进制数字转换为一位八进制数字,运算的顺序是从低位向高位依次进行,高位不足三位用零补齐。
例如:二进制数1011001100转换为八进制数1314

方法: 八进制整数转换为二进制整数时,思路是相反的,每一位八进制数字转换为三位二进制数字,运算的顺序也是从低位向高位依次进行。
例如:八进制数1024转换为二进制数1000010100

5.2、二进制与十六进制之间的转换
二进制整数转换为十六进制整数时,每四位二进制数字转换为一位十六进制数字,运算的顺序是从低位向高位依次进行,高位不足四位用零补齐。
例如:二进制数10110101011100转换为十六进制数2D5C

十六进制整数转换为二进制整数时,思路是相反的,每一位十六进制数字转换为四位二进制数字,运算的顺序也是从低位向高位依次进行。
例如:十六进制数B3A5转换为二进制数1011001110100101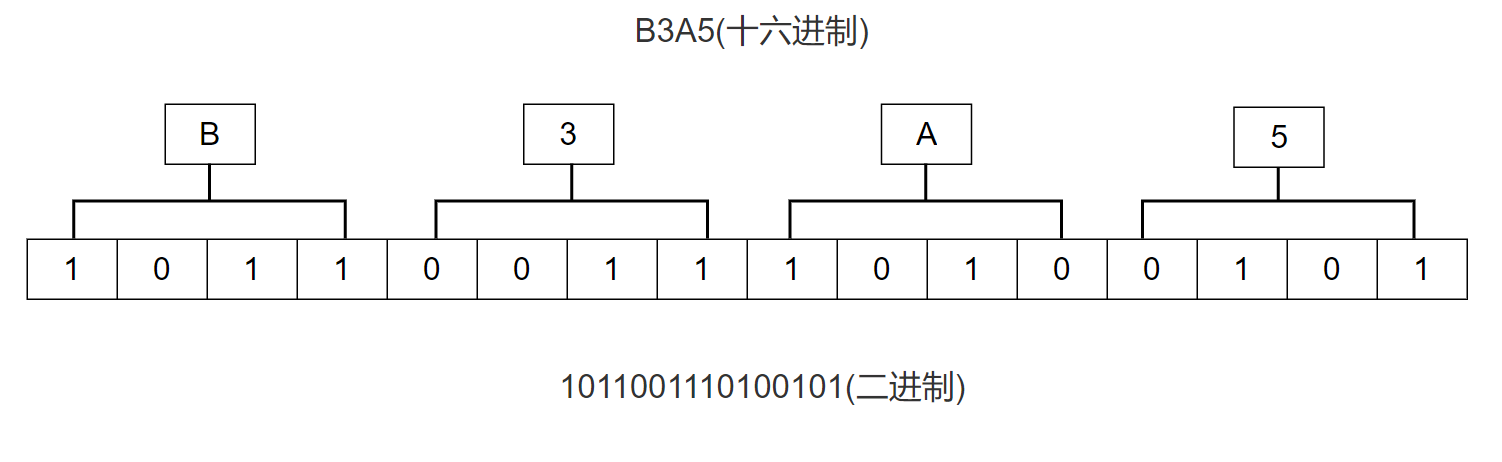
六、常用进制对照表

总结
由于作者水平有限,如笔下有误,敬请留言。
如果本文对您有所帮助,请给博主点赞关注哦,笔者会持续更新干货教程,期待与君共勉!
边栏推荐
猜你喜欢
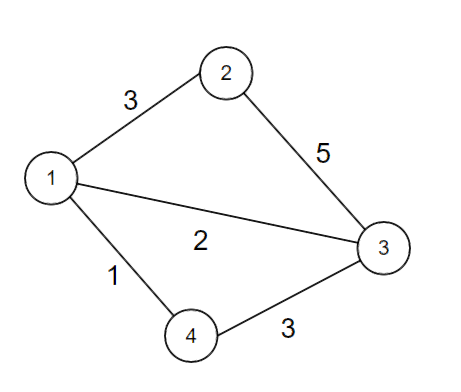
图的拉普拉斯矩阵
Discourse 的关闭主题(Close Topic )和重新开放主题
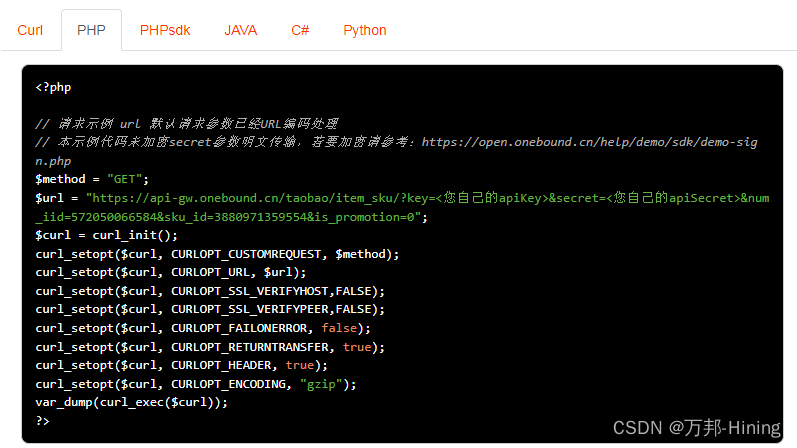
Taobao sku API interface (PHP example)
每日sql--统计员工近三个月的总薪水(不包括最新一个月)

Redis源码:Redis源码怎么查看、Redis源码查看顺序、Redis外部数据结构到Redis内部数据结构查看源码顺序
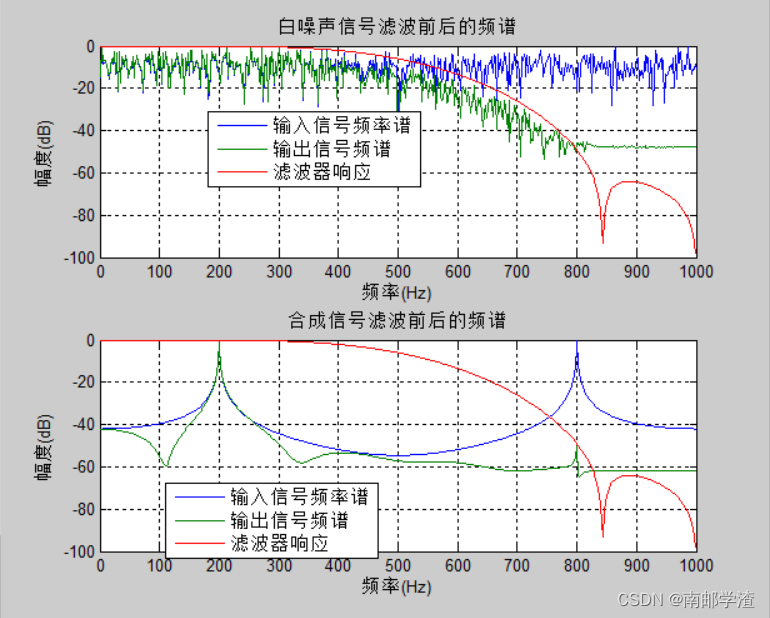
基于FPGA的FIR滤波器的实现(4)— 串行结构FIR滤波器的FPGA代码实现
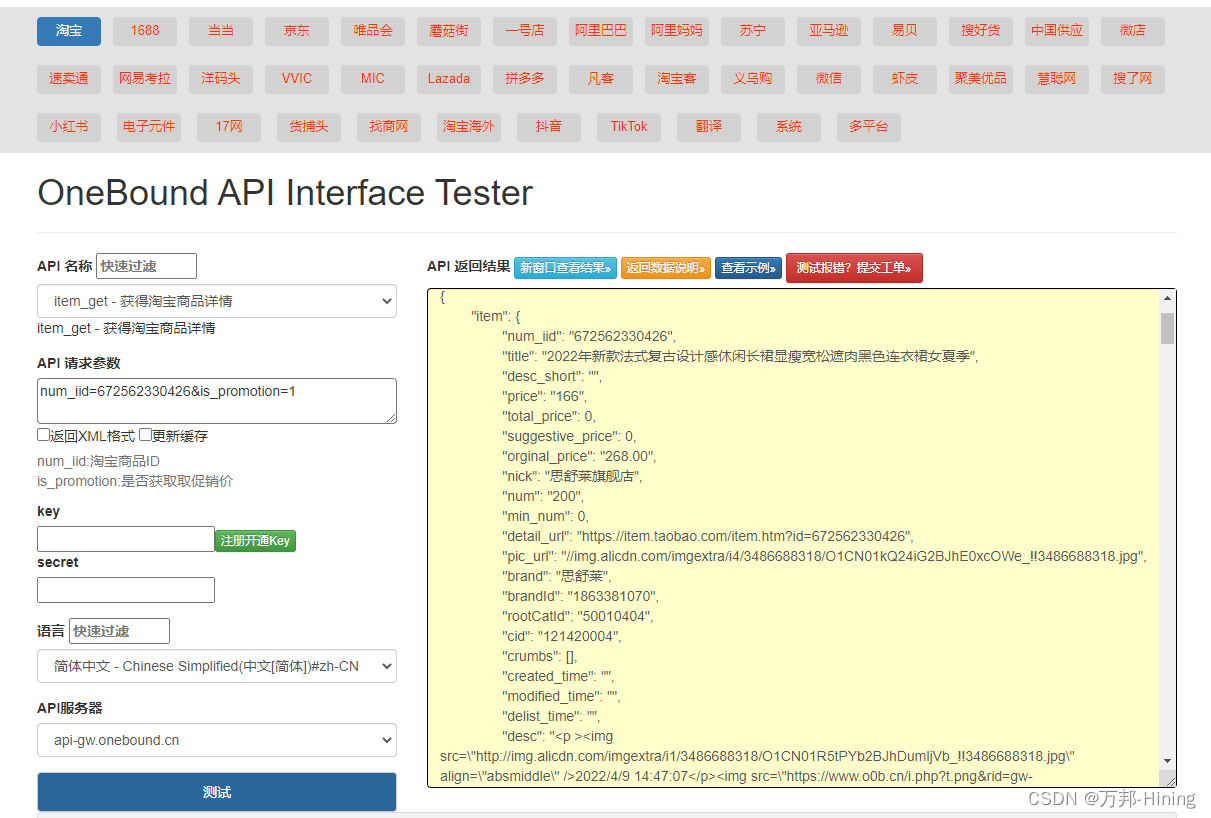
Taobao API common interface and acquisition method
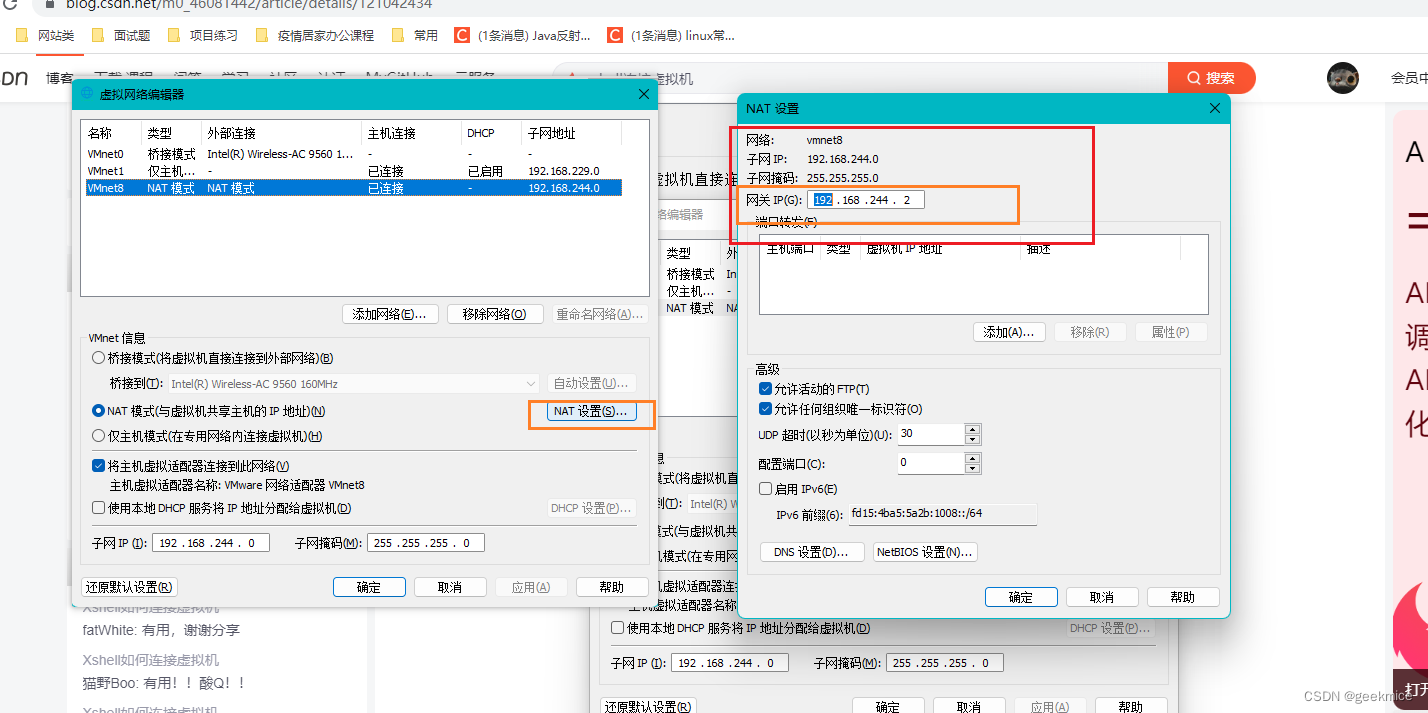
How Xshell connects to a virtual machine
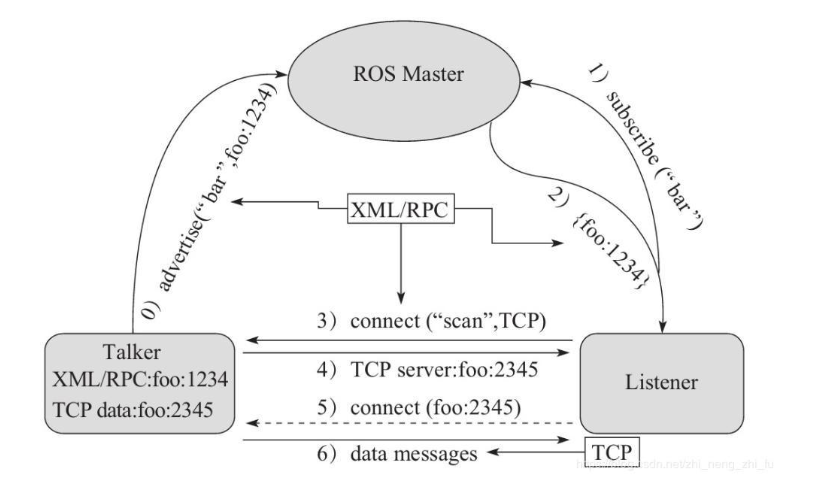
ROS 话题通信理论模型
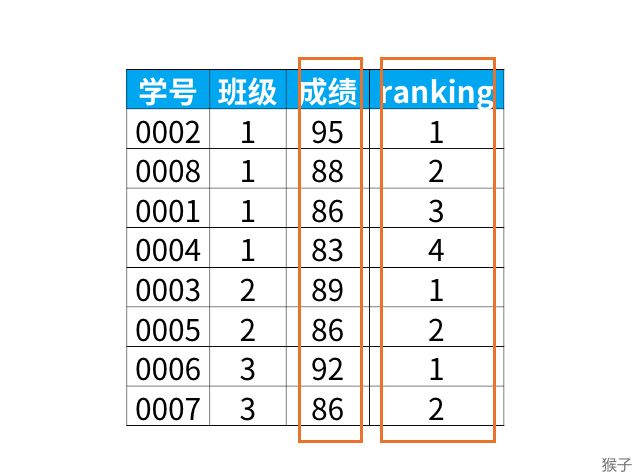
SQL滑动窗口
随机推荐
联想集团:2022/23财年第一季度业绩
一张图了解JVM八大原子操作
Do not add the is prefix to the variables of the boolean type in the POJO class of the Alibaba specification
Redis源码:Redis源码怎么查看、Redis源码查看顺序、Redis外部数据结构到Redis内部数据结构查看源码顺序
daily sql - query for managers and elections with at least 5 subordinates
HCIP Republish/Routing Policy Experiment
Go语言实现Etcd服务发现(Etcd & Service Discovery & Go)
daily sql - user retention rate for two days
Especially the redis
Daily SQL - find each of the students school gpa minimum (window)
空间金字塔池化 -Spatial Pyramid Pooling(含源码)
Implement general-purpose, high-performance sorting and quicksort optimizations
每日sql-统计各个专业人数(包括专业人数为0的)
unable to extend table xxx by 1024 in tablespace xxxx
那些事情是用Unity开发项目应该一开始规划好的?如何避免后期酿成巨坑?
How to choose professional, safe and high-performance remote control software
docker安装mysql5.7(仅供测试使用)
NFT 的价值从何而来
2022-08-09 第四小组 修身课 学习笔记(every day)
矩阵分析——矩阵分解
