当前位置:网站首页>complete knapsack theory
complete knapsack theory
2022-08-10 00:33:00 【empty__barrel】
有N件物品和一个最多能背重量为W的背包.第i件物品的重量是weight[i],得到的价值是value[i] .每件物品都有无限个(也就是可以放入背包多次),求解将哪些物品装入背包里物品价值总和最大.
完全背包和01背包问题唯一不同的地方就是,每种物品有无限件.
我们知道01背包内嵌的循环是从大到小遍历,为了保证每个物品仅被添加一次.
for(int i = 0; i < weight.size(); i++) {
// 遍历物品
for(int j = bagWeight; j >= weight[i]; j--) {
// 遍历背包容量
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
}
}
- 而完全背包的物品是可以添加多次的,所以要从小到大去遍历,即:
// 先遍历物品,再遍历背包
for(int i = 0; i < weight.size(); i++) {
// 遍历物品
for(int j = weight[i]; j <= bagWeight ; j++) {
// 遍历背包容量
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
}
}
遍历顺序:
01背包中二维dp数组的两个for遍历的先后循序是可以颠倒了,一维dp数组的两个for循环先后循序一定是先遍历物品,再遍历背包容量.If you traverse the backpack capacity first and then nest the items, the details are as follows(Traverse horizontally column by column):
The current value is determined by the value above and the value in the upper left corner,In this case, the value of the upper left corner is not known when traversing a value,所以不行.
在完全背包中,对于一维dp数组来说,其实两个for循环嵌套顺序同样无所谓!Because the weight of the backpack is traversed from small to large at this time, the value of the upper left corner can be known at this time.如图(Traverse horizontally column by column)

代码:
先遍历物品,在遍历背包
void test_CompletePack() {
vector<int> weight = {
1, 3, 4};
vector<int> value = {
15, 20, 30};
int bagWeight = 4;
vector<int> dp(bagWeight + 1, 0);
for(int i = 0; i < weight.size(); i++) {
// 遍历物品
for(int j = weight[i]; j <= bagWeight; j++) {
// 遍历背包容量
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
}
}
cout << dp[bagWeight] << endl;
}
int main() {
test_CompletePack();
}
先遍历背包,再遍历物品
void test_CompletePack() {
vector<int> weight = {
1, 3, 4};
vector<int> value = {
15, 20, 30};
int bagWeight = 4;
vector<int> dp(bagWeight + 1, 0);
for(int j = 0; j <= bagWeight; j++) {
// 遍历背包容量
for(int i = 0; i < weight.size(); i++) {
// 遍历物品
if (j - weight[i] >= 0) dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
}
}
cout << dp[bagWeight] << endl;
}
int main() {
test_CompletePack();
}
两个forThe loop nesting order is suitable for different question types:
组合不强调元素之间的顺序,排列强调元素之间的顺序.
如果求组合数就是外层for循环遍历物品,内层for遍历背包.
如果求排列数就是外层for遍历背包,内层for循环遍历物品.
例如:
给定不同面额的硬币和一个总金额.写出函数来计算可以凑成总金额的硬币组合数.假设每一种面额的硬币有无限个.
设定总金额为6,面额数组为coins【1,5】
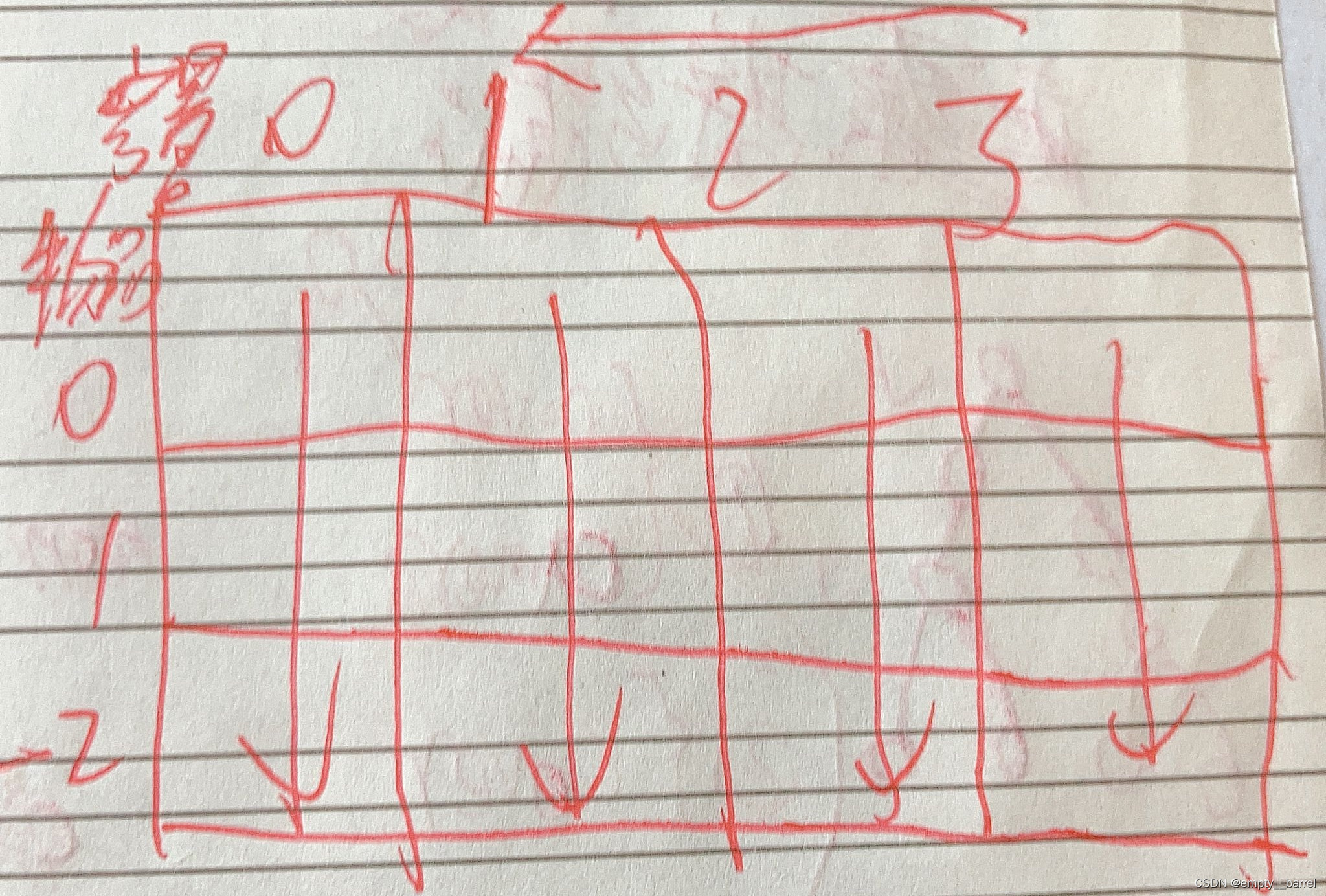
1. The first picture below is the outer layerfor循环遍历物品,内层for遍历背包
若此时求解dp【6】,dp【6】will be solved twice
- 用1A combination of dollars j number of methods at this timedp【6】 = dp【6】+dp【5】 = 1,The key is here and nowdp【5】为1Because the rows are traversed from top to bottom,At this point, only the values in front of the first row are traversed, so this is the casedp【5】The sequence in is just by1组成的原先dp【6】为初始化的dp【6】为0
- 用1块钱和5A combination of dollars j The number of methods is ready to use1A sequence of dollars is composed j 的方法数+用有5A sequence of dollars is composed j 的方法数 dp【6】= dp【6】+dp【1】= 2
2. The second picture below is the inner layerfor遍历背包,外层for循环遍历物品
若此时求解dp【6】,dp【6】will be solved twice
- 用1A combination of dollars j number of methods at this timedp【6】 = dp【6】+dp【5】 = 1,**The key is here and nowdp【5】为2This is because all columns preceding this column are traversed from left to rightdp【5】The sequence in contains more than just by value1构成的序列,Also contains by value5构成的序列,**原先dp【6】为初始化的dp【6】为0
- 用1块钱和5A combination of dollars j The number of methods is ready to use1A sequence of dollars is composed j 的方法数+用有5A sequence of dollars is composed j 的方法数 dp【6】= dp【6】+dp【1】= 2
简单而言,原因就在于
- 当外层for循环遍历物品,内层for遍历背包:计算当前dp的时候,required frontdpThe sequence in is limited to0~The sequence of the current item
- 当内层for遍历背包,外层for循环遍历物品:计算当前dp的时候,required frontdpThe sequence in is completedp是0~物品n的序列
0 ~ n个物品组合成 j 的方法数 = 0 ~ n-1个物品组合成j-coins[n]的方法数+第0~nan itemn组合成 j 的方法数.这是一个递归,When imagining, you can recursively abstract imagination.
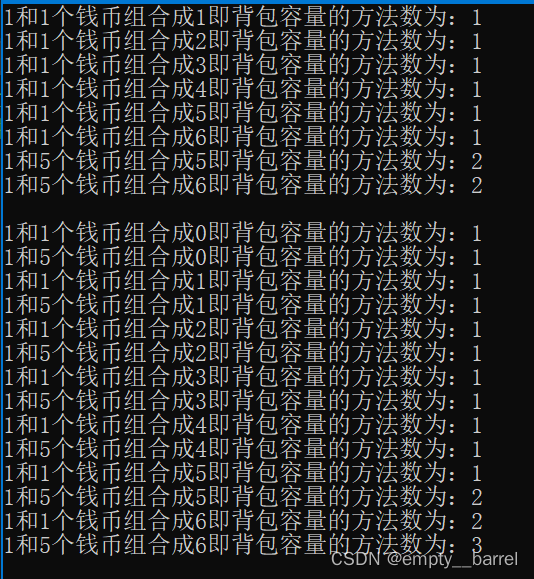
测试代码:
namespace jj01 {
int a()
{
vector<int>coins(2);
coins[0] = 1;
coins[1] = 5;
int amount = 6;
vector<int>dp(7, 0);
dp[0] = 1;
for (int i = 0; i < coins.size(); i++) {
// 遍历物品
for (int j = coins[i]; j <= amount; j++) {
// 遍历背包容量
dp[j] += dp[j - coins[i]];
cout << coins[0] << "和" << coins[i] << "composed of coins" << j << "That is, the number of methods for the knapsack capacity is :" << dp[j] << endl;
//Has the first item combined j 的方法数
//There is a second item combined j The number of methods that is combined without the second itemj-coins[2]的方法数
//0~n个物品组合成j的方法数 = 0~n-1个物品组合成j-coins[n]的方法数+第0~nan itemn组合成j的方法数.
}
}
return 0;
}
}
namespace jj02
{
int a()
{
vector<int>coins(2);
coins[0] = 1;
coins[1] = 5;
int amount = 6;
vector<int>dp(7, 0);
dp[0] = 1;
for (int j = 0; j <= amount; j++) {
// 遍历背包容量
for (int i = 0; i < coins.size(); i++) {
// 遍历物品
if (j - coins[i] >= 0) dp[j] += dp[j - coins[i]];
cout << coins[0] << "和" << coins[i] << "composed of coins" << j << "That is, the number of methods for the knapsack capacity is :" << dp[j] << endl;
//Has the first item combined j 的方法数
//There is a second item combined j The number of methods that is combined without the second itemj-coins[2]的方法数
//0~n个物品组合成j的方法数 = 0~n-1个物品组合成j-coins[n]的方法数+第0~nan itemn组合成j的方法数.
}
}
return 0;
}
}
int main() {
jj01::a();
cout << endl;
jj02::a();
return 0;
}
边栏推荐
猜你喜欢
随机推荐
如何正则匹配乱码?
完全背包理论
2021年国内外五大BI厂商——优秀的商业智能工具推荐
68.qt quick-qml多级折叠下拉导航菜单 支持动态添加/卸载 支持qml/widget加载等
Gold Warehouse Database KingbaseGIS User Manual (6.2. Management Functions)
【接口测试】requests 库请求体字符串解码
HBuilder X 不能运行到内置终端
数字与中文大写数字互转(5千万亿亿亿亿以上的数字也支持转换)
Interfering with BGP routing---community attributes
金仓数据库 KingbaseGIS 使用手册(6.4. 几何对象存取函数)
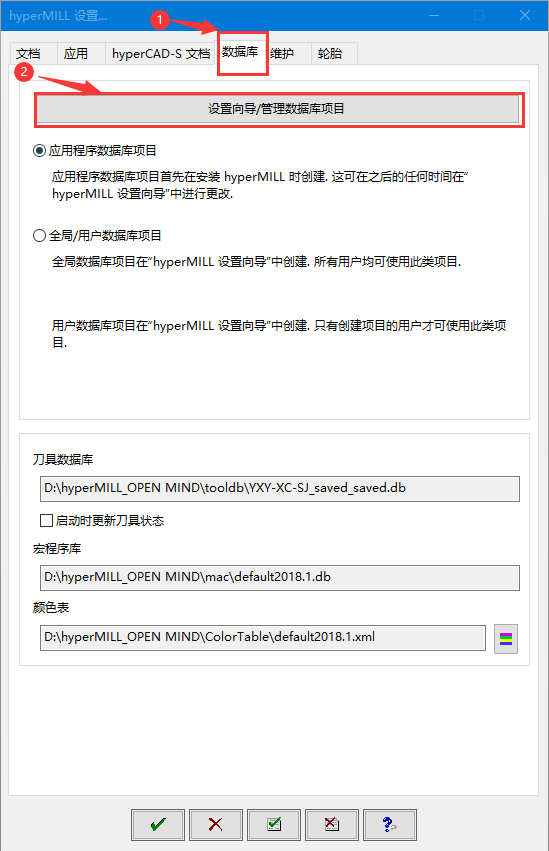
【实用工具系列】MathCAD入门安装及快速上手使用教程
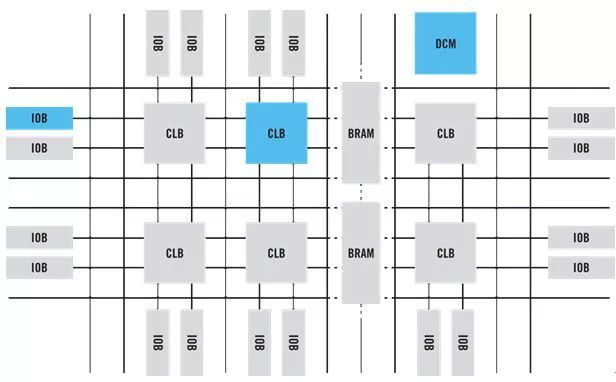
全面解析FPGA基础知识
Gartner全球集成系统市场数据追踪,超融合市场增速第一
力扣:377. 组合总和 Ⅳ
上海一科技公司刷单被罚22万,揭露网络刷单灰色产业链
xlrd 与 xlsxwritter 的基本操作
【AtomicInteger】常规用法
PyQt5:入门使用教程
Filament-Material 绘制基本图形
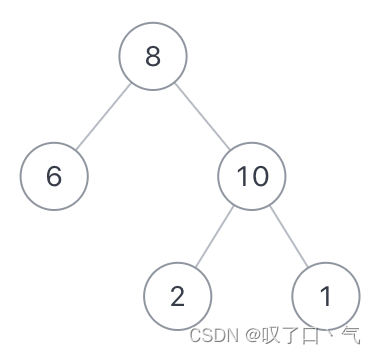
Leetcode 236. 二叉树的最近公共祖先