当前位置:网站首页>Derivation of Σ GL perspective projection matrix
Derivation of Σ GL perspective projection matrix
2022-04-23 16:41:00 【itzyjr】

Computer monitors are two-dimensional surfaces . from OpenGL Rendered 3D The scene must be as 2D The image is projected onto the computer screen . The projection matrix is used for this projection transformation . First , It converts all vertex data from eye coordinates to clipping coordinates . then , By matching with the clipping coordinates w Component division , These clipping coordinates are also converted to normalized device coordinates (NDC).
Clipping coordinates : The eye coordinates are now multiplied by the projection matrix , Become clipping coordinates . The projection matrix defines the visual cone —— How vertex data is projected onto the screen ( Perspective or orthogonal ). It's called clipping coordinates , Because the transformed vertices (x,y,z) It's through talking to ±wclip Cut by comparison .
Cone culling ( tailoring ) The operation is performed in clipping coordinates , Just divided by wclip Before . Through and with wclip Comparison , The clipping coordinates are tested xclip、yclip and zclip. Because divided by wclip Then become normalized NDC coordinate , So to satisfy -1<=xclip/wclip<=1, therefore xclip∈[-wclip,wclip]; Empathy yclip∈[-wclip,wclip],zclip∈[-wclip,wclip]. If any clipping coordinates are less than -wclip Or greater than wclip, The vertex will be discarded ( Cut out ).
therefore , We must remember , tailoring ( Cone culling ) and NDC The transformations are integrated into the projection matrix . Here's how to start from 6 Construct the projection matrix with two parameters :left、right、bottom、top、near and far The boundary value .
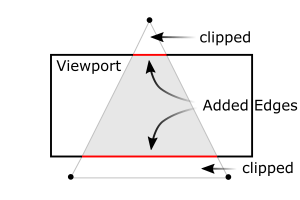
then ,OpenGL The edges of the clipped polygon will be reconstructed ( See the two red lines in the figure below ).
The gray area in the following figure is the point that is reserved but not discarded , Satisfy :xc,yc,zc∈(-wc,wc)
The following figure shows the perspective cone and normalized equipment coordinates (NDC):
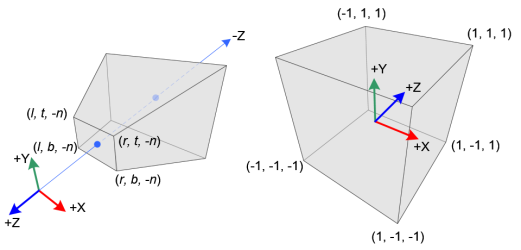
In perspective projection , The cone of the visual cone ( Eye coordinates ) Medium 3D Points are mapped to cubes (NDC);x The coordinates are from [l,r] To [-1,1],y The coordinates are from [b,t] To [-1,1],z The coordinates are from [-n,-f] To [-1,1].
void glFrustum(
// Specify the coordinates of the left and right vertical clipping planes .
GLdouble left, GLdouble right,
// Specify the coordinates of the bottom and top horizontal clipping planes .
GLdouble bottom, GLdouble top,
// Specifies the distance to the near depth clipping plane and the far depth clipping plane . Both distances must be positive .
GLdouble nearVal, GLdouble farVal
);
Please note that , Eye coordinates are defined in the right-hand coordinate system , but NDC Use the left-hand coordinate system . in other words , The camera at the origin moves along in eye space -Z Axis view , But in NDC Middle edge +Z Axis view . because glFrustum() We only accept near and far Positive value of , Therefore, we need to negate them when constructing projection matrices .
stay OpenGL in , One in eye space 3D The point is projected to the near plane ( The projection plane ) On . The following figure shows a point in eye space (xe,ye,ze) How to project to the near plane (xp,yp,zp).
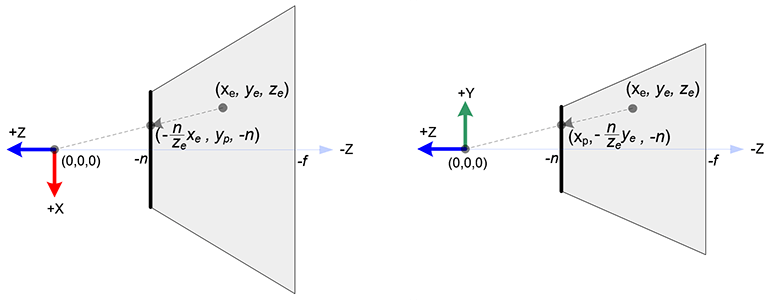
From the of the visual cone [ Top view ], That is, the of eye space x coordinate ,xe Mapped to xp,xp It is calculated by using the ratio of similar triangles :
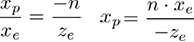
From the side of the visual cone ,yp Calculated in a similar way :
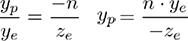
Be careful xp and yp Rely on a ze; They are associated with -ze In inverse proportion . let me put it another way , They are all -ze except . This is the first clue to construct the projection matrix . After transforming the eye coordinates by multiplying the projection matrix , The clipping coordinates are still homogeneous . It eventually becomes standardized equipment coordinates (NDC), Divided by the clipping coordinates w component .( For more details , see OpenGL_Transformation)
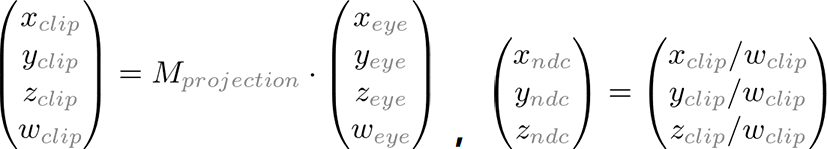
therefore , We can cut the coordinates of w The component is set to -ze. The second of the projection matrix 4 Line into (0,0,-1,0).

Next , We use a linear relationship to describe xp and yp Mapping to NDC Of xn and yn;[l,r]⇒ [-1,1] and [b,t]⇒ [-1,1].

then , We will xp and yp Substitute into the above equation .
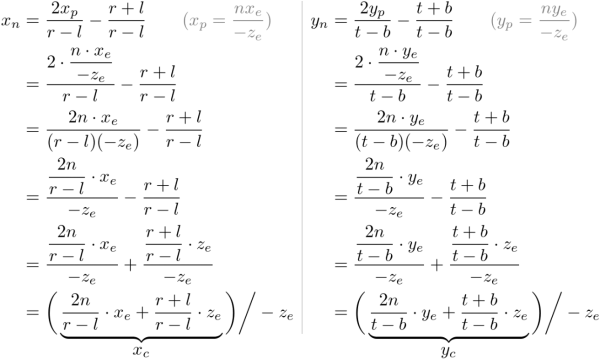
Be careful , For perspective Division (xc/wc,yc/wc), Let's make two terms of each equation be -ze to be divisible by . We will wc Set to -ze, The terms in parentheses become the of clipping coordinates xc and yc.
From these equations , We can find the second of the projection matrix 1 Xing He 2 That's ok .

Now? , We just need to solve the problem 3 Row projection matrix . Find out zn A little different from others , Because of... In eye space ze Always projected onto the near plane -n. But we need the only z Values for clipping and depth testing . Besides , We should be able to cancel the projection ( inverse transformation ). Because we know z Don't depend on x or y value , So we borrow w Component to find zn and ze The relationship between . therefore , We can specify the second of the projection matrix in this way 3 That's ok .
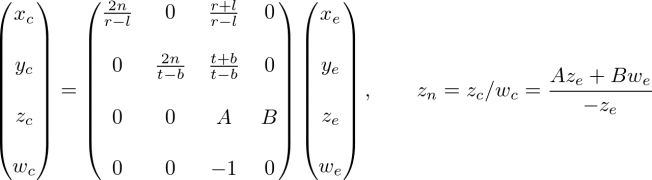
In eye space ,we be equal to 1. therefore , The equation becomes :
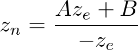
To find the coefficient A and B, We use (ze,zn) Relationship :(-n,-1) and (-f,1), And put them into the above equation , figure out A、B.
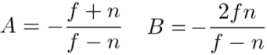
here ,ze And zn The relationship becomes :
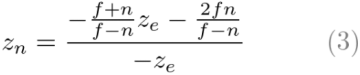
Last , We found all the entries of the projection matrix . The complete projection matrix is :
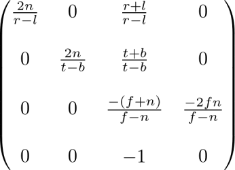
The projection matrix is suitable for general viewing cone . If the visual body is symmetrical , namely r=-l, t=-b, It can be reduced to :
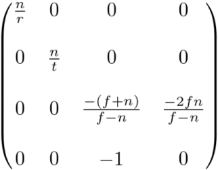
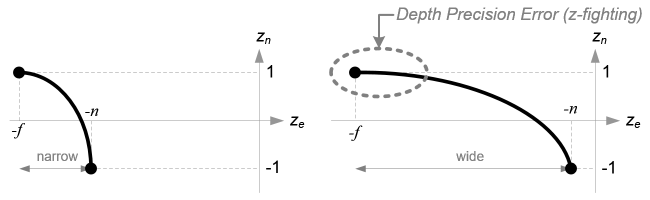
Before we move on , Please look again ze and zn The relationship between , equation (3). You notice that this is a rational function ,ze and zn There is a nonlinear relationship between ( Here's the picture ). This means that the accuracy in the near plane is very high , But the accuracy in the far plane is very low . If the range [-n,-f] More and more big , It will lead to the problem of depth accuracy (z-fighting); Near the far plane ze Small changes in do not affect zn value .n and f The distance between should be as short as possible , To minimize the depth buffer accuracy problem .
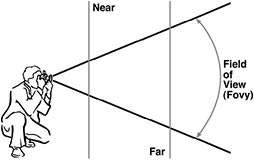
Use FOV Specified perspective projection :
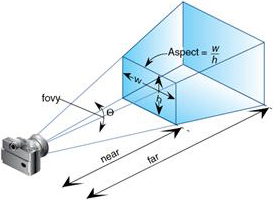
h = 2 × near × tan(θ/2)
w = h × aspect;
Corresponding to the above perspective projection matrix :
r = w/2;t = h/2
therefore :
n/r = (2×n)/w
= (2×n)/(h × aspect)
= (2×n)/(2 × n × tan(θ/2) × aspect)
= cot(θ/2)/aspect
Similarly obtained ,n/t = cot(θ/2)
Then the perspective projection matrix is :
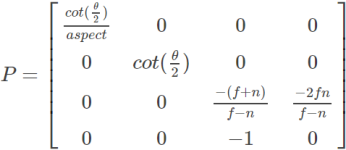
版权声明
本文为[itzyjr]所创,转载请带上原文链接,感谢
https://yzsam.com/2022/04/202204231639280899.html
边栏推荐
- Differences between MySQL BTREE index and hash index
- Modify the test case name generated by DDT
- Loggie source code analysis source file module backbone analysis
- True math problems in 1959 college entrance examination
- MySQL personal learning summary
- Redis "8" implements distributed current limiting and delay queues
- 关于局域网如何组建介绍
- On the security of key passing and digital signature
- Introduction notes to PHP zero Foundation (13): array related functions
- ESXi封装网卡驱动
猜你喜欢
Dancenn: overview of byte self-developed 100 billion scale file metadata storage system

Force buckle-746 Climb stairs with minimum cost

OMNeT学习之新建工程

The solution of not displaying a whole line when the total value needs to be set to 0 in sail software
Nacos detailed explanation, something

Nacos 详解,有点东西
Use case labeling mechanism of robot framework

Deepinv20 installation MariaDB

Sail soft segmentation solution: take only one character (required field) of a string
G008-hwy-cc-estor-04 Huawei Dorado V6 storage simulator configuration
随机推荐
NVIDIA graphics card driver error
JSP learning 3
Deepinv20 installation MariaDB
G008-hwy-cc-estor-04 Huawei Dorado V6 storage simulator configuration
UWA Pipeline 功能详解|可视化配置自动测试
Server log analysis tool (identify, extract, merge, and count exception information)
Best practice of cloud migration in education industry: Haiyun Jiexun uses hypermotion cloud migration products to implement progressive migration for a university in Beijing, with a success rate of 1
人脸识别框架之dlib
File system read and write performance test practice
PyTorch:train模式与eval模式的那些坑
Detailed explanation of UWA pipeline function | visual configuration automatic test
Execution plan calculation for different time types
JIRA screenshot
各大框架都在使用的Unsafe类,到底有多神奇?
Sail soft segmentation solution: take only one character (required field) of a string
Knowledge points and examples of [seven input / output systems]
JMeter setting environment variable supports direct startup by entering JMeter in any terminal directory
100 deep learning cases | day 41 - convolutional neural network (CNN): urbansound 8K audio classification (speech recognition)
The most detailed Backpack issues!!!
JSP learning 1
