当前位置:网站首页>根心与根轴
根心与根轴
2022-08-10 20:31:00 【lvshu】
例题 2.1.1 在凸五边形 中,,, 为五边形内一点,使得 ,,证明:
证法一:
由射影定理,,
故是与的根轴
而的圆心在线段上,所以
证法二:
故是与的根轴
而与的连心线平行于,所以
例题 2.1.2 在 中, < ,点 分别是边 的中点 的内切圆圆心为 ,且与边 相切与点 ,直线 经过线段 的中点且与 垂直,与直线 交于点 ,证明:
证:
记 的外接圆为圆 ,记以 为圆心, 为半径的圆为圆
易知圆 的圆心为 的外接圆中 的中点
由对称性, 分别于 关于直线 对称
因此,点 在圆 与圆 的根轴上,类似地,点 也在这两圆根轴上
从而直线 即为这两个圆的根轴
又因为直线 是点圆 与圆 的根轴
故点 是点圆 ,圆 ,圆 的根心,直线 即为点圆 与圆 的根轴
而事实上,点圆 与圆 的根轴为圆 在点 处的切线,与 垂直
所以
边栏推荐
- The servlet mapping path matching resolution
- 如何提交一个PR?【OpenHarmony成长计划】【OpenHarmony开源社区】
- 七月券商金工精选
- Ferritin particle-loaded raltitrexed/pemetrexed/sulfadesoxine/adamantane (scientific research reagent)
- zip文件协议解析
- 转铁蛋白(Tf)修饰去氢骆驼蓬碱磁纳米脂质体/香豆素-6脂质体/多柔比星脂质体
- C 语言 时间函数使用技巧(汇总)
- 电信保温杯笔记——《统计学习方法(第二版)——李航》第17章 潜在语义分析
- 2021年中国工业互联网安全大赛(福建省选拔赛) 暨首届福建省工业互联网创新大赛
- 报错:runtime error: reference binding to null pointer of type ‘std::vector<int, std::allocator<int>>‘
猜你喜欢
随机推荐
(十二) findContours函数的hierarchy详解
通用线程:POSIX 线程详解,第 2部分
1D Array Dynamics and Question Answers
转铁蛋白(Tf)修饰去氢骆驼蓬碱磁纳米脂质体/香豆素-6脂质体/多柔比星脂质体
"POJ 3666" Making the Grade problem solution (two methods)
sklearn 笔记 TSNE
单选点击可取消功能
leetcode 85.最大矩形 单调栈应用
[CNN] Brush SOTA's trick
Future-oriented IT infrastructure management architecture - Unified IaaS
svg+元素js实现在图片上描点成框,并获取相对图片的坐标位置
【图像分类】2019-MoblieNetV3 ICCV
大小端的理解以及宏定义实现的理解
C语言写数据库
Echart饼状图标注遮盖解决方案汇总
mysql性能监控与执行计划
ctfshow-osint
npm WARN config global `--global`, `--local` are deprecated. Use `--location=global` instead.
CGO 初步认知和基本数据类型转换
Redis命令手册

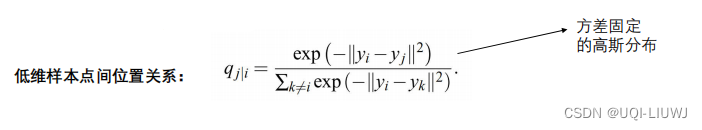
![[SWPUCTF 2021 新生赛] web](/img/e9/07e7db7ddf8328589a078e98fd46ad.png)