当前位置:网站首页>从 GAN 到 WGAN
从 GAN 到 WGAN
2022-08-10 18:39:00 【发呆的比目鱼】
从 GAN 到 WGAN
本文翻译来自:https://lilianweng.github.io/posts/2017-08-20-gan/
生成对抗网络(GAN)在许多生成任务中显示出很好的结果,以复制真实世界的丰富内容,例如图像、人类语言和音乐。它受到博弈论的启发:两个模型,一个生成器和一个判别器,在互相竞争的同时让彼此变得更强大。然而,训练 GAN 模型相当具有挑战性,因为人们面临训练不稳定或无法收敛等问题。
在这里,我想解释一下生成对抗网络框架背后的数学原理,为什么它很难被训练,最后介绍一个旨在解决训练困难的 GAN 的修改版本。
Kullback–Leibler and Jensen–Shannon 散度
在我们开始仔细研究GANs之前,让我们首先回顾用于量化两个概率分布之间相似性的两个指标。
(1) KL (Kullback Leibler)散度衡量一个概率分布 p p p如何偏离第二个期望概率分布 q q q。
D K L ( p ∥ q ) = ∫ x p ( x ) log p ( x ) q ( x ) d x D_{KL}(p \| q) = \int_x p(x) \log \frac{p(x)}{q(x)} dx DKL(p∥q)=∫xp(x)logq(x)p(x)dx
当 p ( x ) = = q ( x ) p(x)== q(x) p(x)==q(x)时,DKL达到最小零。
根据公式可以看出KL散度是不对称的。在 p ( x ) p(x) p(x)接近于零,但 q ( x ) q(x) q(x)显著非零的情况下, q q q的影响被忽略。当我们只是想测量两个同等重要分布之间的相似性时,它可能会导致错误的结果。
(2) Jensen Shannon散度是两个概率分布之间相似性的另一种度量,边界为 [ 0 , 1 ] [0,1] [0,1]。JS的散度是对称的(耶!),更平滑。如果你有兴趣阅读更多关于KL散度和JS散度的比较,请查看Quora上的这篇文章。
D J S ( p ∥ q ) = 1 2 D K L ( p ∥ p + q 2 ) + 1 2 D K L ( q ∥ p + q 2 ) D_{JS}(p \| q) = \frac{1}{2} D_{KL}(p \| \frac{p + q}{2}) + \frac{1}{2} D_{KL}(q \| \frac{p + q}{2}) DJS(p∥q)=21DKL(p∥2p+q)+21DKL(q∥2p+q)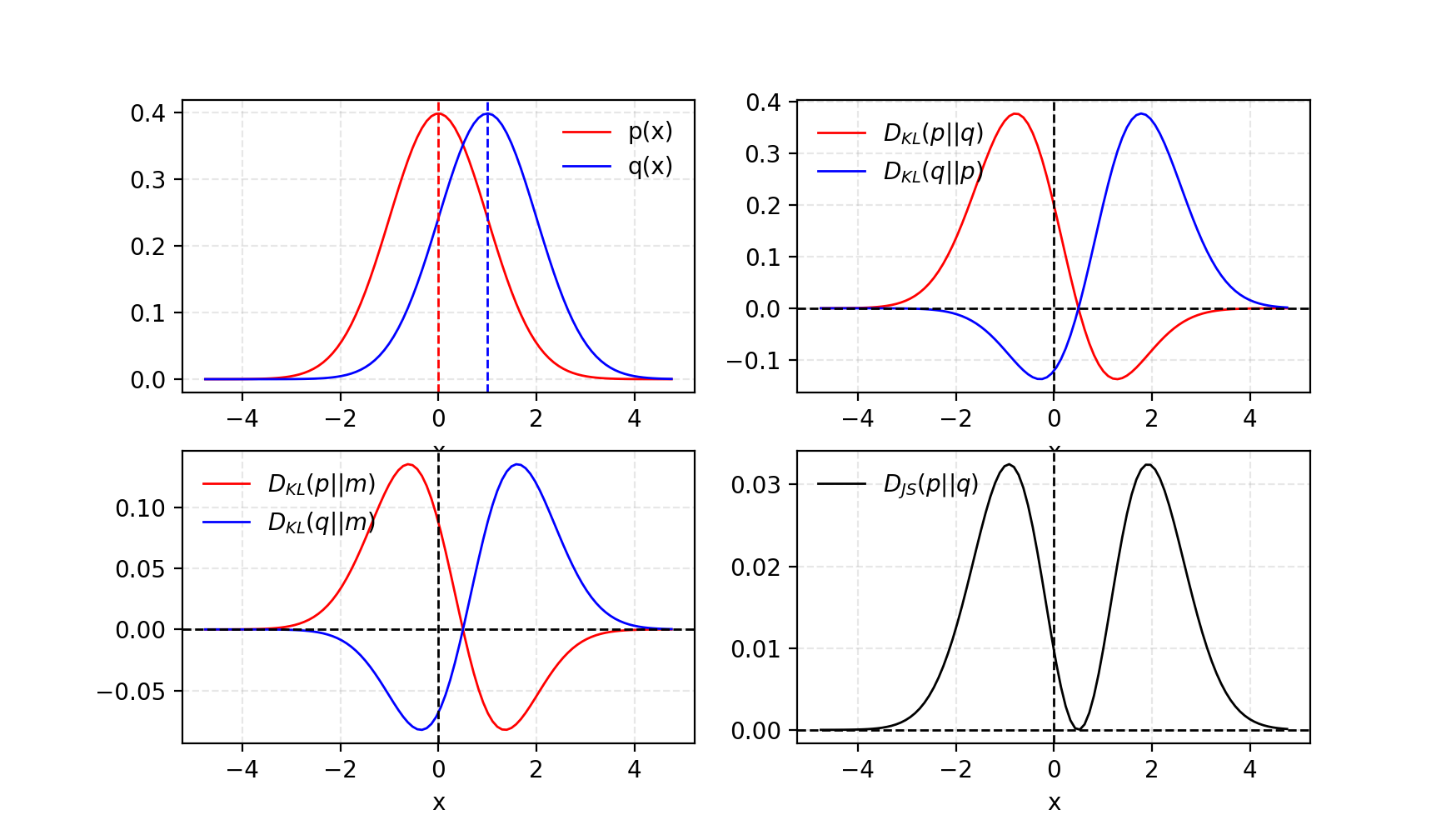
图1, 给定两个高斯分布,p的mean=0, std=1, q的mean=1, std=1。两个分布的平均值被标记为 m = ( p + q ) / 2 m=(p+q)/2 m=(p+q)/2。KL散度 D K L D_{KL} DKL是不对称的,而JS散度 D J S D_{JS} DJS是对称的
一些人认为(Huszar, 2015), GANs大成功背后的一个原因是,将传统最大似然方法中的非对称KL散度的损失函数转换为对称JS散度。我们将在下一节中进一步讨论这一点。
生成对抗网络(GAN)
GAN由两种模型组成
- 鉴别器 D D D估计来自真实数据集的给定样本的概率。它就像一个评论家,优化后可以分辨出假样本和真样本。
- 在给定噪声变量 z z z ( z z z带来潜在输出多样性)的情况下,生成器 G G G输出合成样本。它被训练来捕捉真实的数据分布,这样它的生成样本可以尽可能真实,或者换句话说,可以欺骗鉴别器提供一个高可能性。

图2, 生成式对抗网络的体系结构
这两个模型在训练过程中相互竞争:生成器 G G G努力欺骗判别器,而判别模型 D D D努力不被欺骗。这两个模型之间有趣的零和博弈促使双方都改进其功能。
| 符号 | 意义 | 注释 |
|---|---|---|
| p z p_{z} pz | 数据 z z z在噪声输入上分布 | 通常,只是统一 |
| p g p_{g} pg | 数据 z z z在生成器上分布 | |
| p r p_{r} pr | 数据在真实样本中的分布 |
一方面,我们希望通过最大化 E x ∼ p r ( x ) [ log D ( x ) ] \mathbb{E}_{x \sim p_{r}(x)} [\log D(x)] Ex∼pr(x)[logD(x)]来确保判别器 D D D对真实数据的判断是准确。同时,给定一个假样本 G ( z ) G(z) G(z), z ∼ p z ( z ) z \sim p_z(z) z∼pz(z),期望鉴别器通过最大化 E z ∼ p z ( z ) [ log ( 1 − D ( G ( z ) ) ) ] \mathbb{E}_{z \sim p_{z}(z)} [\log (1 - D(G(z)))] Ez∼pz(z)[log(1−D(G(z)))]输出概率 D ( G ( z ) ) D(G(z)) D(G(z))接近于零。
另一方面,对生成器进行训练,以增加 D D D产生高概率假例子的机会,从而最小化 E z ∼ p z ( z ) [ log ( 1 − D ( G ( z ) ) ) ] \mathbb{E}_{z \sim p_{z}(z)} [\log (1 - D(G(z)))] Ez∼pz(z)[log(1−D(G(z)))]
当把这两个方面结合在一起时, D D D和 G G G正在玩一个极大极小博弈,我们应该优化下面的损失函数:
min G max D L ( D , G ) = E x ∼ p r ( x ) [ log D ( x ) ] + E z ∼ p z ( z ) [ log ( 1 − D ( G ( z ) ) ) ] = E x ∼ p r ( x ) [ log D ( x ) ] + E x ∼ p g ( x ) [ log ( 1 − D ( x ) ] \begin{aligned} \min_G \max_D L(D, G) & = \mathbb{E}_{x \sim p_{r}(x)} [\log D(x)] + \mathbb{E}_{z \sim p_z(z)} [\log(1 - D(G(z)))] \\ & = \mathbb{E}_{x \sim p_{r}(x)} [\log D(x)] + \mathbb{E}_{x \sim p_g(x)} [\log(1 - D(x)] \end{aligned} GminDmaxL(D,G)=Ex∼pr(x)[logD(x)]+Ez∼pz(z)[log(1−D(G(z)))]=Ex∼pr(x)[logD(x)]+Ex∼pg(x)[log(1−D(x)]
E x ∼ p r ( x ) [ log D ( x ) ] \mathbb{E}_{x \sim p_{r}(x)} [\log D(x)] Ex∼pr(x)[logD(x)]在梯度下降更新时对 G G G没有影响。
D的最佳值是多少
现在我们有一个明确定义的损失函数。让我们先看看 D D D的最佳值是多少。
L ( G , D ) = ∫ x ( p r ( x ) log ( D ( x ) ) + p g ( x ) log ( 1 − D ( x ) ) ) d x L(G, D) = \int_x \bigg( p_{r}(x) \log(D(x)) + p_g (x) \log(1 - D(x)) \bigg) dx L(G,D)=∫x(pr(x)log(D(x))+pg(x)log(1−D(x)))dx
因为我们感兴趣的是最大化 L ( G , D ) L(G, D) L(G,D)的 D ( x ) D(x) D(x)最佳值是多少,让我们标记:
x ~ = D ( x ) , A = p r ( x ) , B = p g ( x ) \tilde{x} = D(x), A=p_{r}(x), B=p_g(x) x~=D(x),A=pr(x),B=pg(x)
然后积分内的值(我们可以忽略这个积分因为 x x x是在所有可能的值上抽样的)是
f ( x ~ ) = A l o g x ~ + B l o g ( 1 − x ~ ) d f ( x ~ ) d x ~ = A 1 l n 10 1 x ~ − B 1 l n 10 1 1 − x ~ = 1 l n 10 ( A x ~ − B 1 − x ~ ) = 1 l n 10 A − ( A + B ) x ~ x ~ ( 1 − x ~ ) \begin{aligned} f(\tilde{x}) & = A log\tilde{x} + B log(1-\tilde{x}) \\ \frac{d f(\tilde{x})}{d \tilde{x}} & = A \frac{1}{ln10} \frac{1}{\tilde{x}} - B \frac{1}{ln10} \frac{1}{1 - \tilde{x}} \\ & = \frac{1}{ln10} (\frac{A}{\tilde{x}} - \frac{B}{1-\tilde{x}}) \\ & = \frac{1}{ln10} \frac{A - (A + B)\tilde{x}}{\tilde{x} (1 - \tilde{x})} \\ \end{aligned} f(x~)dx~df(x~)=Alogx~+Blog(1−x~)=Aln101x~1−Bln1011−x~1=ln101(x~A−1−x~B)=ln101x~(1−x~)A−(A+B)x~
因此,设 d f ( x ~ ) d x ~ = 0 \frac{d f(\tilde{x})}{d \tilde{x}} = 0 dx~df(x~)=0,得到判别器的最佳值:
D ∗ ( x ) = x ~ ∗ = A A + B = p r ( x ) p r ( x ) + p g ( x ) ∈ [ 0 , 1 ] D^*(x) = \tilde{x}^* = \frac{A}{A + B} = \frac{p_{r}(x)}{p_{r}(x) + p_g(x)} \in [0, 1] D∗(x)=x~∗=A+BA=pr(x)+pg(x)pr(x)∈[0,1]
当 p g = p r p_g = p_{r} pg=pr等于1/2时,一旦生成器被训练到最优, p g p_g pg就会非常接近 p r p_r pr。
什么是全局最优
当 G G G和 D D D都处于最佳值时, 我们有 p g = p r p_g = p_r pg=pr和 D ∗ ( x ) = 1 / 2 D*(x) = 1/2 D∗(x)=1/2,损耗函数变为:
L ( G , D ∗ ) = ∫ x ( p r ( x ) log ( D ∗ ( x ) ) + p g ( x ) log ( 1 − D ∗ ( x ) ) ) d x = log 1 2 ∫ x p r ( x ) d x + log 1 2 ∫ x p g ( x ) d x = − 2 log 2 \begin{aligned} L(G, D^*) &= \int_x \bigg( p_{r}(x) \log(D^*(x)) + p_g (x) \log(1 - D^*(x)) \bigg) dx \\ &= \log \frac{1}{2} \int_x p_{r}(x) dx + \log \frac{1}{2} \int_x p_g(x) dx \\ &= -2\log2 \end{aligned} L(G,D∗)=∫x(pr(x)log(D∗(x))+pg(x)log(1−D∗(x)))dx=log21∫xpr(x)dx+log21∫xpg(x)dx=−2log2
损失函数代表什么
根据上节列出的公式, p r p_r pr和 p g p_g pg之间的JS散度可以计算为
D J S ( p r ∥ p g ) = 1 2 D K L ( p r ∣ ∣ p r + p g 2 ) + 1 2 D K L ( p g ∣ ∣ p r + p g 2 ) = 1 2 ( log 2 + ∫ x p r ( x ) log p r ( x ) p r + p g ( x ) d x ) + 1 2 ( log 2 + ∫ x p g ( x ) log p g ( x ) p r + p g ( x ) d x ) = 1 2 ( log 4 + L ( G , D ∗ ) ) \begin{aligned} D_{JS}(p_{r} \| p_g) =& \frac{1}{2} D_{KL}(p_{r} || \frac{p_{r} + p_g}{2}) + \frac{1}{2} D_{KL}(p_{g} || \frac{p_{r} + p_g}{2}) \\ =& \frac{1}{2} \bigg( \log2 + \int_x p_{r}(x) \log \frac{p_{r}(x)}{p_{r} + p_g(x)} dx \bigg) + \\& \frac{1}{2} \bigg( \log2 + \int_x p_g(x) \log \frac{p_g(x)}{p_{r} + p_g(x)} dx \bigg) \\ =& \frac{1}{2} \bigg( \log4 + L(G, D^*) \bigg) \end{aligned} DJS(pr∥pg)===21DKL(pr∣∣2pr+pg)+21DKL(pg∣∣2pr+pg)21(log2+∫xpr(x)logpr+pg(x)pr(x)dx)+21(log2+∫xpg(x)logpr+pg(x)pg(x)dx)21(log4+L(G,D∗))
因此;
L ( G , D ∗ ) = 2 D J S ( p r ∥ p g ) − 2 log 2 L(G, D^*) = 2D_{JS}(p_{r} \| p_g) - 2\log2 L(G,D∗)=2DJS(pr∥pg)−2log2
GAN的损失函数本质上是在鉴别器最优时,通过JS散度量化生成数据分布 p g p_g pg与真实样本分布 p r p_r pr之间的相似性。复制真实数据分布的最佳 G ∗ G^* G∗导致最小 L ( G ∗ , D ∗ ) = − 2 log 2 L(G^*, D^*) = -2\log2 L(G∗,D∗)=−2log2,这与上面的方程对齐。
GAN的其他变体: 在不同的上下文中或为不同的任务设计了许多GANs变体。例如,对于半监督学习,一种想法是更新鉴别器,输出真实的类标签, 1 ,, K − 1 1,,K-1 1,,K−1,以及一个假的类标签 K K K。生成器模型的目的是欺骗鉴别器输出一个小于K的分类标签。
Tensorflow执行:carpedm20/DCGAN-tensorflow
Gans的问题
虽然GAN在真实感图像生成方面取得了巨大的成功,但训练并不容易;这个过程被认为是缓慢和不稳定的。
难以达到Nash平衡
Salimans等人(2016)讨论了GAN基于梯度下降的训练过程的问题。同时训练两个模型来寻找一个二人非合作博弈的Nash均衡。然而,每个模型都独立更新其成本,而不考虑游戏中的其他玩家。同时更新两个模型的梯度不能保证收敛。
让我们通过一个简单的例子来更好地理解为什么在非合作博弈中很难找到Nash均衡。假设一个玩家控制 x x x以最小化 f 1 ( x ) = x y f_1(x) = xy f1(x)=xy,同时另一个玩家不断更新 y y y以最小化 f 2 ( y ) = − x y f_2(y) = -xy f2(y)=−xy。
因为 ∂ f 1 ∂ x = y \frac{\partial f_1}{\partial x} = y ∂x∂f1=y, ∂ f 2 ∂ y = − x \frac{\partial f_2}{\partial y} = -x ∂y∂f2=−x,我们在一次迭代中同时更新x为 x − η ⋅ y x-\eta \cdot y x−η⋅y,更新 y y y为 y + η ⋅ x y+ \eta \cdot x y+η⋅x,其中 η \eta η为学习率。一旦 x x x和 y y y有不同的符号,后续的梯度更新都会引起巨大的振荡,不稳定性在时间上变得更差,如图3所示。
图3示例,更新 x x x以最小化 x y xy xy,更新 y y y以最小化 − x y -xy −xy。学习率 η = 0.1 \eta = 0.1 η=0.1。随着迭代次数的增加,振荡变得越来越不稳定。
低维的支持
| Term | 解释 |
|---|---|
| manifold | 在每一点附近局部类似欧几里得空间的拓扑空间。准确地说,当欧几里得空间的维数为n时,这个流形称为n流形。 |
| Support | 一个实值函数f是域的子集,它包含那些没有映射到零的元素。 |
Arjovsky和Bottou(2017)在一篇非常理论化的论文中讨论了 p r p_r pr和 p g p_g pg在低维manifolds上的支持问题,以及它如何导致GAN训练的不稳定性。
许多真实世界数据集的维度,如 p r p_r pr所表示的,似乎只是人为地偏高。人们发现它们可以集中在低维manifolds中。这实际上是多元学习的基本假设。思考现实世界的图像,一旦主题或所包含的对象固定下来,图像就会有很多的限制,比如狗要有两只耳朵和一条尾巴,摩天大楼要有一个挺括高大的身体等等。这些限制使得图像无法具有高维自由形式。
P g P_g Pg也存在于低维manifolds中。每当生成器被要求在给定小维(比如100)的情况下获得64x64这样的大图像时,噪声变量输入 z z z, 4096个像素上的颜色分布就被定义为小的100维随机数向量,很难填满整个高维空间。当它们有不相交的支持时,我们总是能够找到一个完美的鉴别器,100%正确地区分真实和虚假样本。如果你对证明感到好奇, 参考如下Paper。
图4, 高维空间中的低维流形几乎不可能有重叠。(左)三维空间中的两条线。(右)三维空间中的两个曲面。
梯度消失
当判别器是完美的,我们保证 D ( x ) = 1 , ∀ x ∈ p r D(x) = 1, \forall x \in p_r D(x)=1,∀x∈pr和 D ( x ) = 0 , ∀ x ∈ p g D(x) = 0, \forall x \in p_g D(x)=0,∀x∈pg。因此,损失函数 L L L降为零,在学习迭代过程中,我们最终没有梯度来更新损失。图5展示了一个实验,当判别器越好,梯度消失得越快。
图5所示, 首先,DCGAN被训练为1、10和25个epoch。然后,在生成器固定的情况下,从头训练一个判别器,用原始代价函数测量梯度。我们看到梯度规范衰减迅速(对数尺度),在最好的情况下,经过4000次判别器迭代后5个数量级。(图片来源:Arjovsky and Bottou, 2017)
因此,训练GAN面临着一个两难的境地:
- 如果判别器性能不佳,则生成器反馈不准确,损失函数不能反映实际情况。
- 如果判别器做得很好,损失函数的梯度下降到接近于零,学习变得超级慢,甚至是阻塞。
这种困境显然使GAN训练变得非常困难。
模式崩溃
在训练期间,生成器可能会崩溃到一个设置,它总是产生相同的输出。这是GANs常见的故障情况,通常称为模式崩溃。尽管生成器可能能够欺骗相应的鉴别器,但它无法学会表示复杂的现实世界数据分布,并被卡在一个变化极低的小空间里。
图6所示,一个DCGAN模型是用一个4层、512个单元和ReLU激活功能的MLP网络进行训练的,该网络配置为对图像生成缺乏强烈的诱导偏差。结果表明,该模型具有显著的模态坍塌程度。(图片来源:Arjovsky, Chintala, & Bottou, 2017)
缺乏适当的评估指标
生成式对抗网络并没有一个好的目标函数来告诉我们训练的进度。没有一个好的评估指标,这就像在黑暗中工作。没有好迹象告诉什么时候停止;没有很好的指标来比较多个模型的性能。
为了稳定和提高GANs的训练,提出以下建议。
前五种方法是实现GAN训练更快收敛的实用技术,提出"Improve Techniques for Training GANs"。最后两种方法是针对不相交分布问题提出"Towards principled methods for training generative adversarial networks"。
(1)特征匹配
特征匹配建议优化判别器,检查生成器的输出是否与真实样本的期望统计量相匹配。在这种情况下,新的损失函数定义为 ∣ E x ∼ p r f ( x ) − E z ∼ p z ( z ) f ( G ( z ) ) ∣ 2 2 | \mathbb{E}_{x \sim p_r} f(x) - \mathbb{E}_{z \sim p_z(z)}f(G(z)) |_2^2 ∣Ex∼prf(x)−Ez∼pz(z)f(G(z))∣22, 其中 f ( x ) f(x) f(x)可以是任何统计特征的计算,如平均值或中位数。
(2)Minibatch歧视
利用小批量判别,该判别器能够在一批中消化训练数据点之间的关系,而不是单独处理每个点。
在一个小批中,我们近似每对样本 c ( x i , x j ) c(x_i, x_j) c(xi,xj)之间的亲密度,通过对同一个数据点与同一批中其他样本的接近程度求和,得到该数据点的总体汇总 o ( x i ) = ∑ j c ( x i , x j ) o(x_i) = \sum_{j} c(x_i, x_j) o(xi)=∑jc(xi,xj)。然后将 o ( x i ) o(x_i) o(xi)显式地添加到模型的输入中。
(3)Historical Averaging
对于这两个模型,在loss函数中添加 ∣ Θ − 1 t ∑ i = 1 t Θ i ∣ 2 | \Theta - \frac{1}{t} \sum_{i=1}^t \Theta_i |^2 ∣Θ−t1∑i=1tΘi∣2,其中 Θ \Theta Θ是模型参数, Θ i \Theta_i Θi是在过去的训练时间 i i i中参数的配置方式。
(4)单向标签平滑
在输入判别器时,不提供1和0标签,而是使用软化值,比如0.9和0.1。结果表明,该方法可以降低网络的脆弱性。
(5)虚拟批归一化(VBN)
每个数据样本都是基于一个固定的批(参考批)数据而不是其小批数据进行规范化的。参考批在开始时选择一次,在训练过程中保持不变。
Theano Implementation: openai/improved-gan
(6)添加噪音
根据上一节的讨论,我们现在知道 p r p_r pr和 p g p_g pg在高维空间中是不相交的,它会导致梯度消失的问题。为了人为地分散分布,并为两个概率分布产生重叠创造更高的机会,一种解决方案是在判别器 D D D的输入上添加连续的噪声。
(7)使用更好的分布相似性度量
vanilla GAN的损失函数测量 p r p_r pr和 p g p_g pg分布之间的JS散度。当两个分布不相交时,这个度量不能提供一个有意义的值。
由于Wasserstein度量具有更平滑的值空间,因此提出用它来代替JS散度。
Wasserstein GAN (WGAN)
Wasserstein的距离是什么
Wasserstein距离是两个概率分布之间距离的度量。它也被称为“ Earth Mover距离”(EM距离的缩写),因为它可以被非正式地解释为将一堆泥土从一个概率分布的形状移动到另一个概率分布的形状所需的最小能量消耗。代价用:移动的泥土量x移动的距离来量化。
让我们先来看一个概率域是离散的简单情况。举个例子,假设我们有两个分布 P P P和 Q Q Q,每个分布有4堆土,都有10铲土。每个土堆的铲数分配如下:
P 1 = 3 , P 2 = 2 , P 3 = 1 , P 4 = 4 Q 1 = 1 , Q 2 = 2 , Q 3 = 4 , Q 4 = 3 P_1 = 3, P_2 = 2, P_3 = 1, P_4 = 4\\ Q_1 = 1, Q_2 = 2, Q_3 = 4, Q_4 = 3 P1=3,P2=2,P3=1,P4=4Q1=1,Q2=2,Q3=4,Q4=3
为了使 P P P看起来像 Q Q Q,如图7所示,我们:
- 首先将2铲从 P 1 P_1 P1移到 P 2 P_2 P2 => ( P 1 , Q 1 ) (P_1, Q_1) (P1,Q1)匹配。
- 然后将2铲从 P 2 P_2 P2移到 P 3 P_3 P3 => ( P 2 , Q 2 ) (P_2, Q_2) (P2,Q2)匹配。
- 最后将1铲从 Q 3 Q_3 Q3移到 Q 4 Q_4 Q4 => ( P 3 , Q 3 ) (P_3,Q_3) (P3,Q3)和 ( P 4 , Q 4 ) (P_4,Q_4) (P4,Q4)匹配。
如果我们将使 P i P_i Pi和 Q i Q_i Qi匹配的成本标记为 δ i \delta_i δi,我们将得到 δ i + 1 = δ i + P i − Q i \delta_{i+1} = \delta_i + P_i - Q_i δi+1=δi+Pi−Qi,在示例中:
δ 0 = 0 δ 1 = 0 + 3 − 1 = 2 δ 2 = 2 + 2 − 2 = 2 δ 3 = 2 + 1 − 4 = − 1 δ 4 = − 1 + 4 − 3 = 0 \begin{aligned} \delta_0 &= 0\\ \delta_1 &= 0 + 3 - 1 = 2\\ \delta_2 &= 2 + 2 - 2 = 2\\ \delta_3 &= 2 + 1 - 4 = -1\\ \delta_4 &= -1 + 4 - 3 = 0 \end{aligned} δ0δ1δ2δ3δ4=0=0+3−1=2=2+2−2=2=2+1−4=−1=−1+4−3=0
最后,搬运工的距离是 W = ∑ ∣ δ i ∣ = 5 W = \sum \vert \delta_i \vert = 5 W=∑∣δi∣=5
图7所示,一步一步的计划,在 P P P和 Q Q Q的桩之间移动泥土,使他们匹配。
当处理连续概率域时,距离公式变为
W ( p r , p g ) = inf γ ∼ Π ( p r , p g ) E ( x , y ) ∼ γ [ ∥ x − y ∥ ] W(p_r, p_g) = \inf_{\gamma \sim \Pi(p_r, p_g)} \mathbb{E}_{(x, y) \sim \gamma}[\| x-y \|] W(pr,pg)=γ∼Π(pr,pg)infE(x,y)∼γ[∥x−y∥]
上式中 Π ( p r , p g ) \Pi(p_r, p_g) Π(pr,pg)是 p r p_r pr与 p g p_g pg之间所有可能的联合概率分布的集合。联合分布 γ ∈ Π ( p r , p g ) \gamma \in \Pi(p_r, p_g) γ∈Π(pr,pg)描述了一个尘埃传输计划,与上面的离散例子相同,但在连续概率空间中。精确地说, γ ( x , y ) \gamma(x, y) γ(x,y)表示污垢的百分比应该从点 x x x运输到 y y y,以便使 x x x遵循 y y y相同的概率分布。这就是为什么 x x x上的边际分布加起来是 p g ′ p_{g'} pg′, ∑ x γ ( x , y ) = p g ( y ) \sum_{x} \gamma(x, y) = p_g(y) ∑xγ(x,y)=pg(y)(一旦我们完成了从每一个可能的 x x x到目标 y y y的计划量的污垢,我们最终得到了确切的 y y y根据 p g p_g pg.),反之亦然, ∑ y γ ( x , y ) = p r ( x ) \sum_{y} \gamma(x, y) = p_r(x) ∑yγ(x,y)=pr(x)。
以 x x x为起点,以 y y y为终点时,移动的泥土总量为 γ ( x , y ) \gamma(x, y) γ(x,y),移动距离为 ∣ x − y ∣ | x-y | ∣x−y∣,因此代价为 γ ( x , y ) ⋅ ∣ x − y ∣ \gamma(x, y) \cdot | x-y | γ(x,y)⋅∣x−y∣。所有 ( x , y ) (x,y) (x,y)对的期望平均成本可以很容易地计算为:
∑ x , y γ ( x , y ) ∥ x − y ∥ = E x , y ∼ γ ∥ x − y ∥ \sum_{x, y} \gamma(x, y) \| x-y \| = \mathbb{E}_{x, y \sim \gamma} \| x-y \| x,y∑γ(x,y)∥x−y∥=Ex,y∼γ∥x−y∥
最后,我们取所有污垢移动方案中代价最小的那个作为EM距离。在Wasserstein距离的定义中, i n f inf inf(下限值,也称为最大下界)表示我们只对最小的代价感兴趣。
为什么Wasserstein比JS或KL发散更好
即使两个分布位于没有重叠的低维流形中,Wasserstein距离仍然可以提供一个有意义的和平滑的之间的距离表示。
WGAN的论文用一个简单的例子来说明这个想法。
假设我们有两个概率分布, P P P和 Q Q Q:
∀ ( x , y ) ∈ P , x = 0 and y ∼ U ( 0 , 1 ) ∀ ( x , y ) ∈ Q , x = θ , 0 ≤ θ ≤ 1 and y ∼ U ( 0 , 1 ) \forall (x, y) \in P, x = 0 \text{ and } y \sim U(0, 1)\\ \forall (x, y) \in Q, x = \theta, 0 \leq \theta \leq 1 \text{ and } y \sim U(0, 1)\\ ∀(x,y)∈P,x=0 and y∼U(0,1)∀(x,y)∈Q,x=θ,0≤θ≤1 and y∼U(0,1)
当 θ ≠ 0 \theta \neq 0 θ=0
D K L ( P ∥ Q ) = ∑ x = 0 , y ∼ U ( 0 , 1 ) 1 ⋅ log 1 0 = + ∞ D K L ( Q ∥ P ) = ∑ x = θ , y ∼ U ( 0 , 1 ) 1 ⋅ log 1 0 = + ∞ D J S ( P , Q ) = 1 2 ( ∑ x = 0 , y ∼ U ( 0 , 1 ) 1 ⋅ log 1 1 / 2 + ∑ x = 0 , y ∼ U ( 0 , 1 ) 1 ⋅ log 1 1 / 2 ) = log 2 W ( P , Q ) = ∣ θ ∣ \begin{aligned} D_{KL}(P \| Q) &= \sum_{x=0, y \sim U(0, 1)} 1 \cdot \log\frac{1}{0} = +\infty \\ D_{KL}(Q \| P) &= \sum_{x=\theta, y \sim U(0, 1)} 1 \cdot \log\frac{1}{0} = +\infty \\ D_{JS}(P, Q) &= \frac{1}{2}(\sum_{x=0, y \sim U(0, 1)} 1 \cdot \log\frac{1}{1/2} + \sum_{x=0, y \sim U(0, 1)} 1 \cdot \log\frac{1}{1/2}) = \log 2\\ W(P, Q) &= |\theta| \end{aligned} DKL(P∥Q)DKL(Q∥P)DJS(P,Q)W(P,Q)=x=0,y∼U(0,1)∑1⋅log01=+∞=x=θ,y∼U(0,1)∑1⋅log01=+∞=21(x=0,y∼U(0,1)∑1⋅log1/21+x=0,y∼U(0,1)∑1⋅log1/21)=log2=∣θ∣
但当 θ = 0 θ=0 θ=0时,两个分布完全重叠
D K L ( P ∥ Q ) = D K L ( Q ∥ P ) = D J S ( P , Q ) = 0 W ( P , Q ) = 0 = ∣ θ ∣ \begin{aligned} D_{KL}(P \| Q) &= D_{KL}(Q \| P) = D_{JS}(P, Q) = 0\\ W(P, Q) &= 0 = \lvert \theta \rvert \end{aligned} DKL(P∥Q)W(P,Q)=DKL(Q∥P)=DJS(P,Q)=0=0=∣θ∣
当两个分布不相交时, D K L D_{KL} DKL给了我们无限大。在 θ = 0 θ=0 θ=0时, D J S D_{JS} DJS的值有突变,不可微。只有Wasserstein度量提供了一个平滑的度量,这对使用梯度下降的稳定学习过程非常有帮助。
使用Wasserstein距离作为GAN损失函数
计算 inf γ ∼ Π ( p r , p g ) \inf_{\gamma \sim \Pi(p_r, p_g)} infγ∼Π(pr,pg)时,很难找出 Π ( p r , p g ) \Pi(p_r, p_g) Π(pr,pg)中所有可能的联合分布。因此,作者提出了一种基于坎托罗维奇-鲁宾斯坦对偶的智能变换公式:
W ( p r , p g ) = 1 K sup ∥ f ∥ L ≤ K E x ∼ p r [ f ( x ) ] − E x ∼ p g [ f ( x ) ] W(p_r, p_g) = \frac{1}{K} \sup_{\| f \|_L \leq K} \mathbb{E}_{x \sim p_r}[f(x)] - \mathbb{E}_{x \sim p_g}[f(x)] W(pr,pg)=K1∥f∥L≤KsupEx∼pr[f(x)]−Ex∼pg[f(x)]
其中 s u p sup sup (supremum)是 i n f inf inf (infomum)的反义词;我们想要测量最小上界,或者更简单地说,最大值。
Lipschitz的连续性?
新形式的Wasserstein度量中的函数 f f f需要满足 ∣ f ∣ L ≤ K | f |_L \leq K ∣f∣L≤K,这意味着它应该是K- lipschitz连续的。
实值函数 f : R → R f: \mathbb{R} \rightarrow \mathbb{R} f:R→R被称为K- lipschitz连续如果存在一个实常数 K ≥ 0 K \geq 0 K≥0,对于所有的 x 1 , x 2 ∈ R x_1, x_2 \in \mathbb{R} x1,x2∈R:
∣ f ( x 1 ) − f ( x 2 ) ∣ ≤ K ∣ x 1 − x 2 ∣ \lvert f(x_1) - f(x_2) \rvert \leq K \lvert x_1 - x_2 \rvert ∣f(x1)−f(x2)∣≤K∣x1−x2∣
这里 K K K被称为函数 f ( . ) f(.) f(.)的Lipschitz常数。处处可连续微的函数是Lipschitz连续的,因为导数,估计为 ∣ f ( x 1 ) − f ( x 2 ) ∣ ∣ x 1 − x 2 ∣ \frac{\lvert f(x_1) - f(x_2) \rvert}{\lvert x_1 - x_2 \rvert} ∣x1−x2∣∣f(x1)−f(x2)∣,有界。然而,一个Lipschitz连续函数可能不是处处可微的,例如 f ( x ) = ∣ x ∣ f(x) = \lvert x \rvert f(x)=∣x∣。
在Wasserstein距离公式上解释转换是如何发生的就足够写一篇长文了,所以我在这里跳过细节。如果你对如何使用线性规划计算Wasserstein 感兴趣,或者如何根据Kantorovich-Rubinstein对偶性将Wasserstein规转换成对偶形式感兴趣,请阅读这篇很棒的文章。
假设这个函数 f f f来自K-Lipschitz连续函数族, { f w } w ∈ W \{ f_w \}_{w \in W} { fw}w∈W,参数为 w w w。在改进的Wasserstein-GAN算法中,通过判别器模型学习 w w w来找到合适的 f w f_w fw,并配置损失函数来测量 p r p_r pr和 p g p_g pg之间的Wasserstein距离。
L ( p r , p g ) = W ( p r , p g ) = max w ∈ W E x ∼ p r [ f w ( x ) ] − E z ∼ p r ( z ) [ f w ( g θ ( z ) ) ] L(p_r, p_g) = W(p_r, p_g) = \max_{w \in W} \mathbb{E}_{x \sim p_r}[f_w(x)] - \mathbb{E}_{z \sim p_r(z)}[f_w(g_\theta(z))] L(pr,pg)=W(pr,pg)=w∈WmaxEx∼pr[fw(x)]−Ez∼pr(z)[fw(gθ(z))]
因此,判别者不再是一个直接的批评家来区分假样本和真样本。相反,它被训练学习K-Lipschitz连续函数来帮助计算Wasserstein距离。随着训练过程中损失函数的减小,Wasserstein距离变小,生成模型的输出更接近真实数据分布。
一个大问题是如何在训练中保持 f w f_w fw的 K K K-Lipschitz连续性,以使一切顺利。本文提出了一个简单但非常实用的技巧:在每次梯度更新后,将权值 w w w夹到一个小窗口,如 [ − 0.01 , 0.01 ] [-0.01, 0.01] [−0.01,0.01],从而得到一个紧致的参数空间 W W W,从而 f w f_w fw得到其下界和上界,以保持Lipschitz连续性。
图9所示, Wasserstein生成式对抗网络算法。(图片来源:Arjovsky, Chintala, & Bottou, 2017)
与原始GAN算法相比,WGAN进行了以下改动:
- 每次对临界函数进行梯度更新后,将权重夹到一个小的固定范围内 [ − c , c ] [-c, c] [−c,c]。
- 用一个新的从Wasserstein 距离推导出来的损失函数,不再用对数。鉴别器模型不是直接的批评家,而是在真实数据分布和生成数据分布之间估计Wasserstein度量的助手。
- 根据经验,作者推荐了RMSProp优化器,而不是基于动量的优化器,如Adam,这可能会导致模型训练中的不稳定。在这一点上,我还没有看到清晰的理论解释。
遗憾的是,Wasserstein GAN并不完美。甚至WGAN的原始论文作者也提到"Weight clipping is a clearly terrible way to enforce a Lipschitz constraint"。WGAN仍然存在训练不稳定、权重剪切后收敛缓慢(当剪切窗口太大时)、梯度消失(当剪切窗口太小时)等问题。
Gulrajani等人在2017年讨论了一些改进,用梯度惩罚精确地取代了重量剪切。
Example: Create New Pokemons!
在一个小数据集(Pokemon Sprites)上尝试Carpedm20/dcgan-tensorflow。这个数据集只有900多张精灵宝可梦图像,包括不同级别的相同精灵宝可梦物种。
让我们看看这个模型能创造出哪些类型的口袋妖怪。遗憾的是,由于训练数据很少,新的口袋妖怪只有粗略的形状,没有细节。训练时间越长,形状和颜色就越好看!万岁
图10.在一组口袋妖怪精灵图像上,训练CarpedM20/dcgan-tensorflow。在epoch= 7、21、49之后列出样品输出。
如果您对CarpedM20/dcgan-Tensorflow的评论版本感兴趣,以及如何对其进行修改以训练WGAN和WGAN以梯度惩罚,请检查Lilianweng/Unified-Gan-Tensorflow。
边栏推荐
猜你喜欢

瑞吉外卖学习笔记4

企业即时通讯是什么?可以应用在哪些场景?
多线程与高并发(五)—— 源码解析 ReentrantLock
![[Image segmentation] Image segmentation based on cellular automata with matlab code](/img/f7/2fd7dfc0bc59bf3492b304c69bd4c7.png)
[Image segmentation] Image segmentation based on cellular automata with matlab code
[教你做小游戏] 只用几行原生JS,写一个函数,播放音效、播放BGM、切换BGM

【Knowledge Sharing】What is SEI in the field of audio and video development?

选择是公有云还或是私有云,这很重要吗?

搭载2.8K 120Hz OLED华硕好屏 无畏Pro15 2022锐龙版屏开得胜
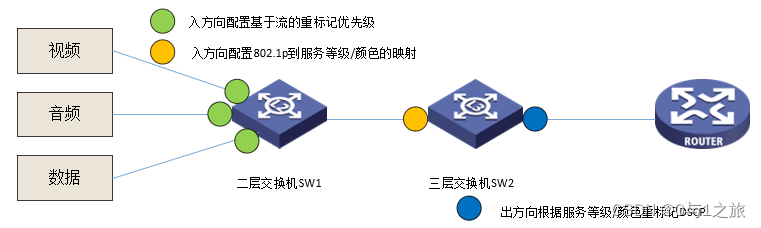
QoS服务质量七交换机拥塞管理
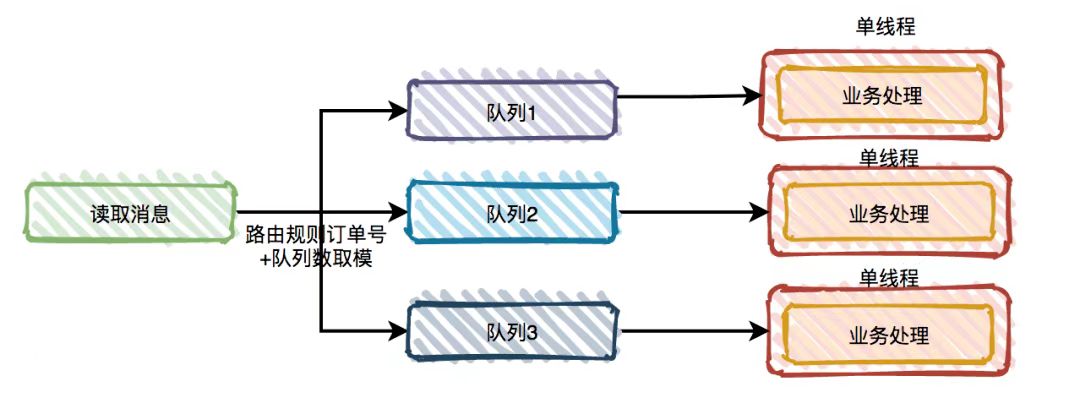
消息队列初见:一起聊聊引入系统mq 之后的问题
随机推荐
Interface test advanced interface script using -apipost (pre/post execution script)
【FAQ】OpenHarmony与HarmonyOS的有什么区别?
LeetCode·283.移除零·双指针
【图像分割】基于元胞自动机实现图像分割附matlab代码
CAS:2055042-70-9_N-(叠氮基-PEG4)-生物素
set和map使用讲解
请问下在datastream中用flinkcdc怎么设置jdbc的参数useSSL=false呀
【Knowledge Sharing】What is SEI in the field of audio and video development?
剑指 Offer 27. 二叉树的镜像(翻转二叉树)
Redis 持久化机制
优化是一种习惯●出发点是'站在靠近临界'的地方
Win11如何清除最近打开过的文件记录?
JVM基本结构
弘玑Cyclone与风变科技达成战略合作:优势互补聚焦数字化人才培养
三星Galaxy Watch5产品图片流出 非Pro表款亦有蓝宝石加持
类型和id对应的两个数组
基于 RocksDB 实现高可靠、低时延的 MQTT 数据持久化
搭建自己的以图搜图系统 (一):10 行代码搞定以图搜图
6-12 二叉搜索树的操作集(30分)
pytorch使用Dataloader加载自己的数据集train_X和train_Y
![[教你做小游戏] 只用几行原生JS,写一个函数,播放音效、播放BGM、切换BGM](/img/30/714d803d4087f5c9c5800a969055fe)