当前位置:网站首页>[problem solving] [show2012] random tree
[problem solving] [show2012] random tree
2022-04-23 16:52:00 【Ants looking up at the stars】
probability / expect dp Basic questions .
There is a binary tree background .
There are two things worth learning about this problem trick .
First look at the first question . Suppose there is i − 1 i-1 i−1 Leaf node , The average depth of each node is f i − 1 f_{i-1} fi−1 .
Then randomly select a node to copy . The expected depth of this node is f i − 1 f_{i-1} fi−1
therefore f i = ( i − 1 ) f i − 1 + f i − 1 + 2 i = f i − 1 + 2 i f_{i}=\frac{(i-1)f_{i-1}+f_{i-1}+2}{i}=f_{i-1}+\frac{2}{i} fi=i(i−1)fi−1+fi−1+2=fi−1+i2
Let's look at the second question .
set up g [ i ] [ j ] g[i][j] g[i][j] Express i i i Second expansion , The depth of the final tree ≥ j \geq j ≥j Of probability .
So the expected depth of the tree ∑ i = 1 n − 1 g [ n − 1 ] [ i ] \sum_{i=1}^{n-1}g[n-1][i] ∑i=1n−1g[n−1][i]
The total number of schemes observed is ( i − 1 ) ! (i-1)! (i−1)! , If the left subtree k k k Time , Right subtree i − k − 1 i-k-1 i−k−1 Time , that p = k ! ( i − k − 1 ) ! ( i − 1 k ) i ! = 1 i p=\frac{k!(i-k-1)!\binom{i-1}{k}}{i!}=\frac{1}{i} p=i!k!(i−k−1)!(ki−1)=i1 .
So according to probability / The expectation formula , g [ i ] [ j ] = ∑ k = 0 i − 1 g [ k ] [ j ] + g [ i − k − 1 ] [ j ] − g [ k ] [ j ] ∗ g [ i − k − 1 ] [ j ] i g[i][j]=\frac{\sum_{k=0}^{i-1}g[k][j]+g[i-k-1][j]-g[k][j]*g[i-k-1][j]}{i} g[i][j]=i∑k=0i−1g[k][j]+g[i−k−1][j]−g[k][j]∗g[i−k−1][j]
Time complexity O ( n 3 ) O(n^3) O(n3) .
#include<bits/stdc++.h>
#define db double
using namespace std;
const int N=105;
db dp[N],dp2[N][N];
int n,Q;
int main() {
for(int i=1;i<=100;i++) {
dp[i]=dp[i-1]+2.0/(i+1);
}
for(int i=0;i<=100;i++) dp2[i][0]=1;
for(int i=1;i<=100;i++) {
for(int j=1;j<=i;j++) {
for(int k=0;k<i;k++) {
dp2[i][j]+=(dp2[k][j-1]+dp2[i-k-1][j-1]-dp2[k][j-1]*dp2[i-k-1][j-1])/i;
}
}
}
scanf("%d%d",&Q,&n);
if(Q==1) printf("%lf",dp[n-1]);
else {
db res=0;
for(int i=1;i<=n-1;i++) {
res+=dp2[n-1][i];
}
printf("%lf",res);
}
}
版权声明
本文为[Ants looking up at the stars]所创,转载请带上原文链接,感谢
https://yzsam.com/2022/04/202204231649165891.html
边栏推荐
- PyMySQL
- 面试百分百问到的进程,你究竟了解多少
- 众昂矿业:萤石浮选工艺
- Mock test using postman
- Nifi fast installation and file synchronization
- 5-minute NLP: text to text transfer transformer (T5) unified text to text task model
- How vscode compares the similarities and differences between two files
- Creation of RAID disk array and RAID5
- loggie 源码分析 source file 模块主干分析
- 5分钟NLP:Text-To-Text Transfer Transformer (T5)统一的文本到文本任务模型
猜你喜欢
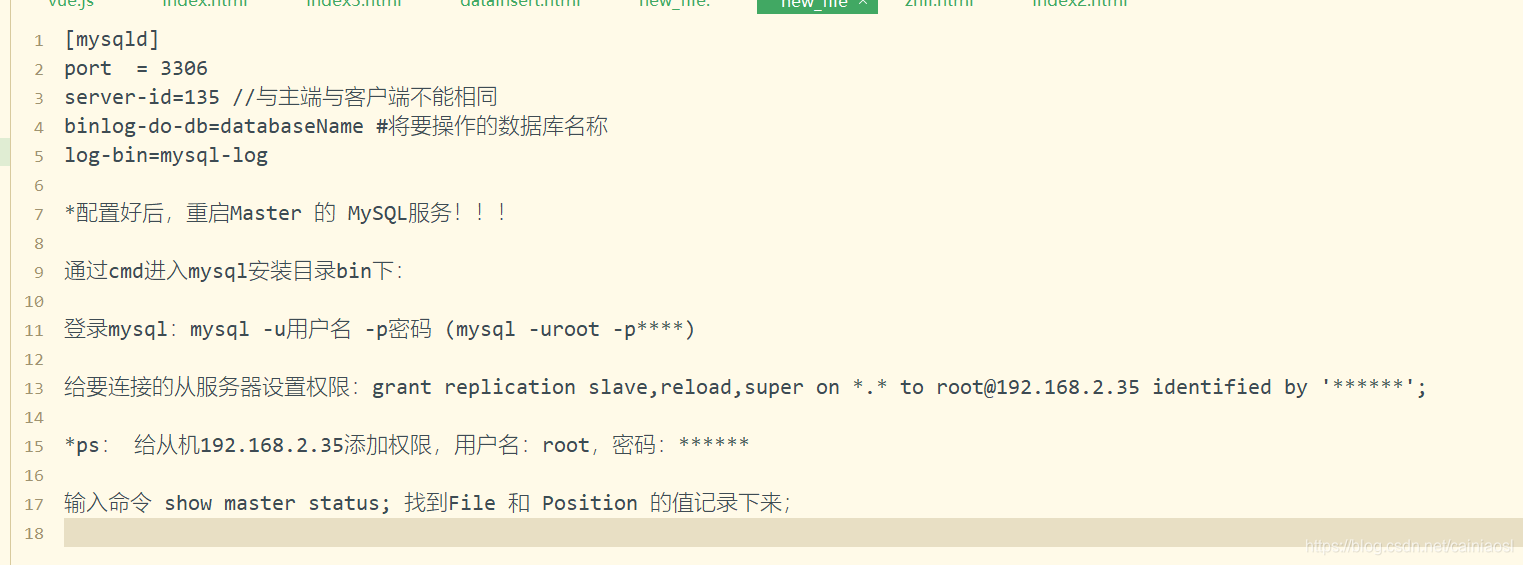
MySQL master-slave synchronization pit avoidance version tutorial
ByteVCharts可视化图表库,你想要的我都有
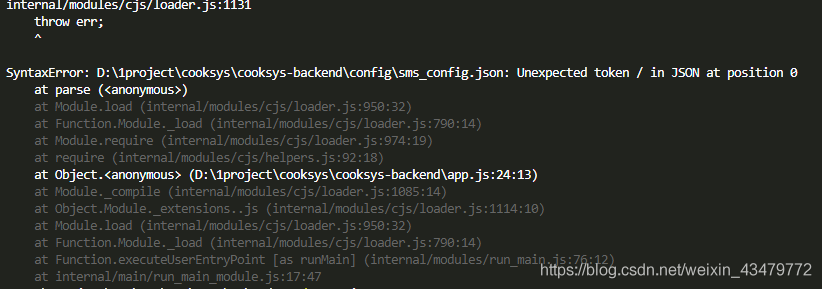
Nodejs reads the local JSON file through require. Unexpected token / in JSON at position appears
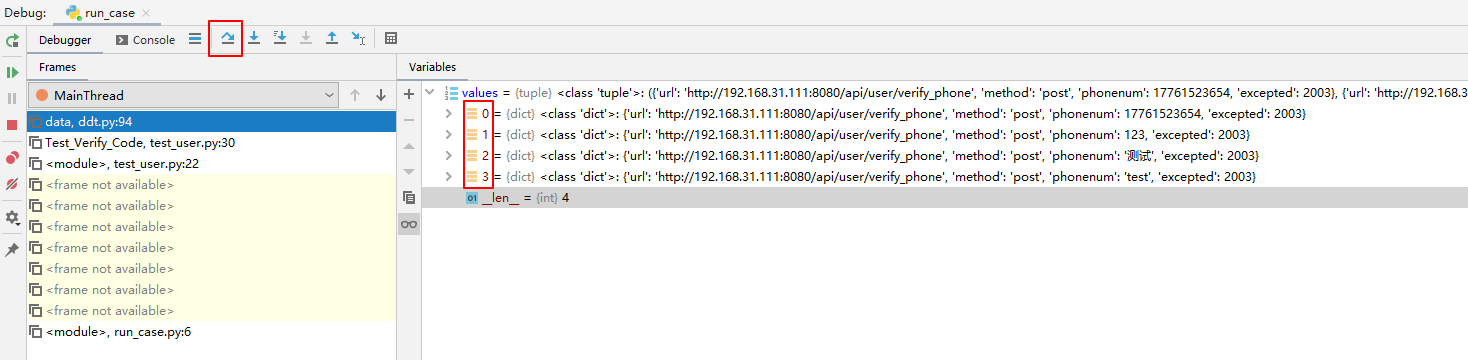
Modify the test case name generated by DDT
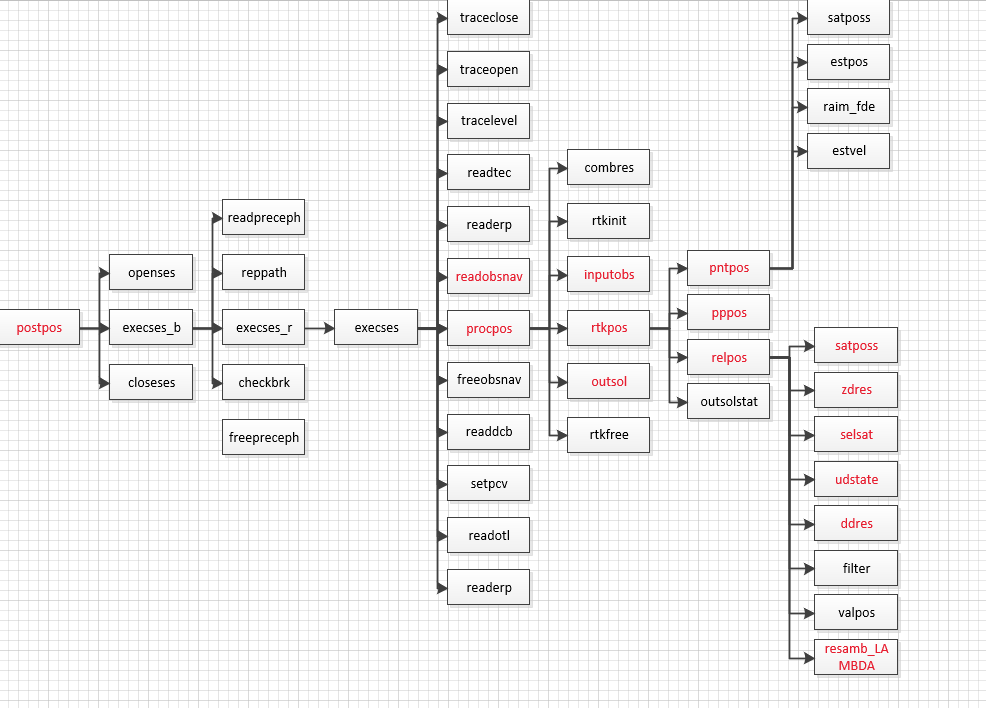
Rtklib 2.4.3 source code Notes
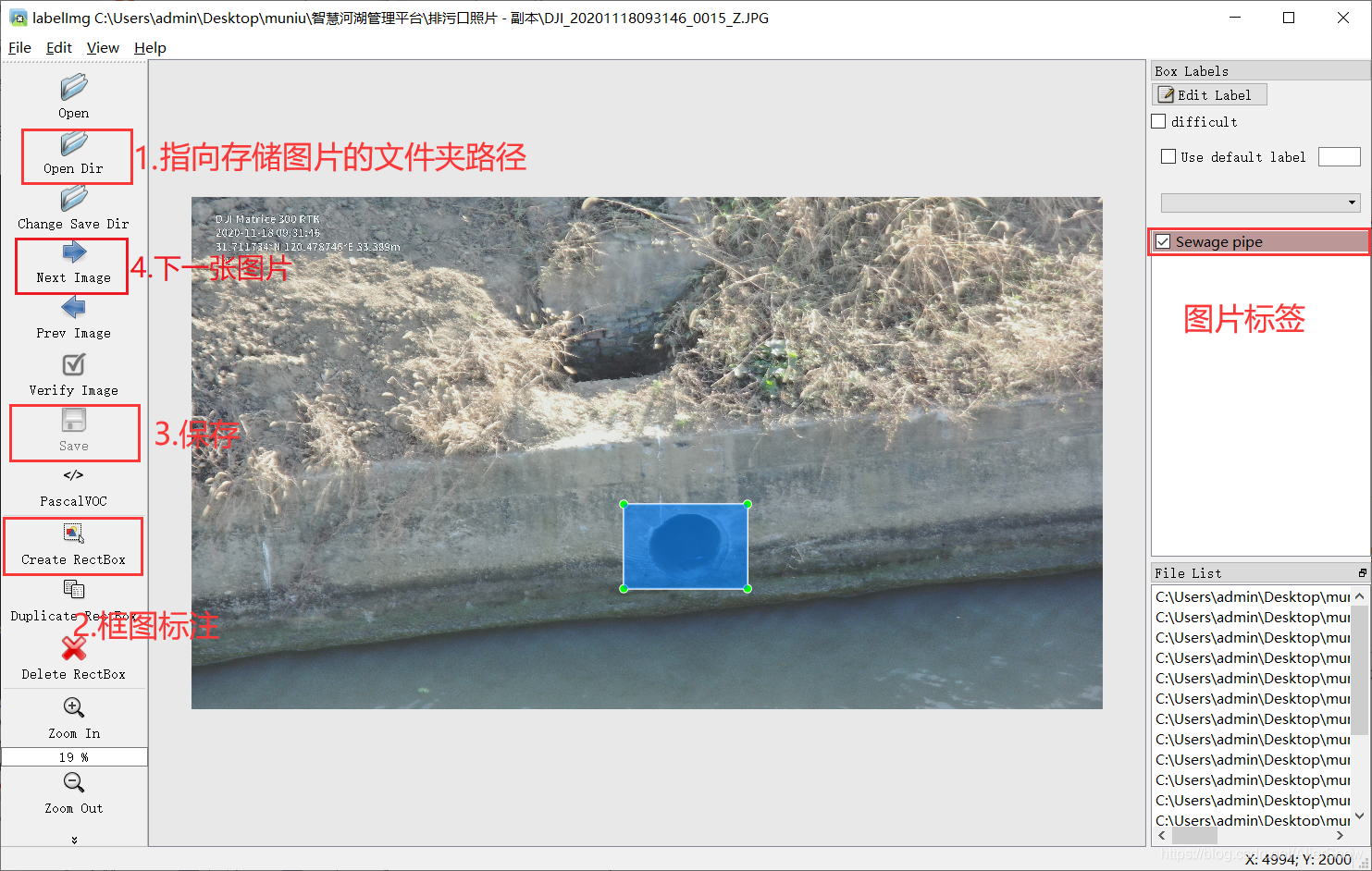
Installing labellmg tutorial in Windows
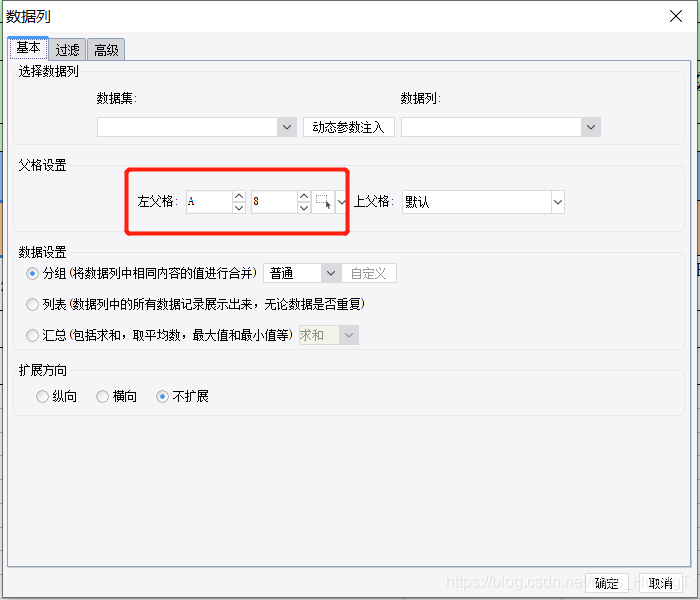
Take according to the actual situation, classify and summarize once every three levels, and see the figure to know the demand
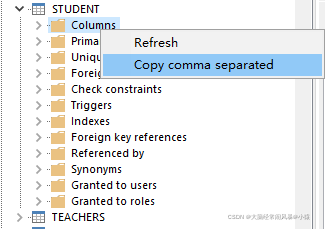
oracle 中快速获取表的列名列表
STM32__03—初识定时器
Pytorch: the pit between train mode and eval mode
随机推荐
PyMySQL
MySQL master-slave replication
Loggie source code analysis source file module backbone analysis
建站常用软件PhpStudy V8.1图文安装教程(Windows版)超详细
关于 background-image 渐变gradient()那些事!
PHP高效读大文件处理数据
Feign report 400 processing
MySql主从复制
Use itextpdf to intercept the page to page of PDF document and divide it into pieces
阿里研发三面,面试官一套组合拳让我当场懵逼
面试百分百问到的进程,你究竟了解多少
Camtasia2022软件新增功能介绍
Derivation of Σ GL perspective projection matrix
SQL database
Nifi fast installation and file synchronization
安装及管理程序
Nodejs installation and environment configuration
How to choose the wireless gooseneck anchor microphone and handheld microphone scheme
Blue Bridge Cup provincial road 06 -- the second game of the 12th provincial competition
About background image gradient()!