About SVM The principle and why SVM Always choose the big one margin Decide the boundary , I'm in the article ：
https://blog.csdn.net/qq_42902997/article/details/124310782
It is expounded in , If you don't understand, you can review

review SVM The goal of optimization

$$C{\Sigma }_{i=1}^m{y}_{i}cos{t}_1({\theta }^T{x}_i)+(1-y_i)cos{t}_0({\theta }^T{x}_i)+\frac{1}{2}{\Sigma }_{j=1}^n{\theta }_j^2(1)$$

• We all know SVM Is a linear classifier , Then face the following linear inseparable scene ：
  
• If you want to implement classification , Then it is absolutely impossible to use a linear classifier to realize , Therefore, we want to introduce polynomials to construct higher-order features to achieve the purpose of the final nonlinear classification .
• Look at the formula given in the figure ; For all the characteristics of a sample x ⃗ = { x 1 , x 2 } \vec{x}=\{x_1,x_2\} x ={ x1​,x2​}; Try to make higher-order features based on these features $x_1{x}_2,x_1^2,x_2^2$ And so on to construct a nonlinear decision boundary ：
  
• Well, along this line , We use a more general form to express , Because our goal is to make higher-order features , So we use ${\theta }_0+{\theta }_1{f}_1+{\theta }_2{f}_2+...+{\theta }_n{f}_n$ To represent our decision boundary ; among $n$ Is the number of features we end up using ; And these $f_1,f_2,...,f_n$ It's the new feature we're going to use .
• In the example above ,$f_1=x_1,f_2=x_2,f_3=x_1{x}_2,f_4=x_1^2,f_5=x_2^2,...$
• Now comes the question , How to ensure that we $f_1,...,f_n$ Is it effective ？

How to construct $f_1,...,f_n$

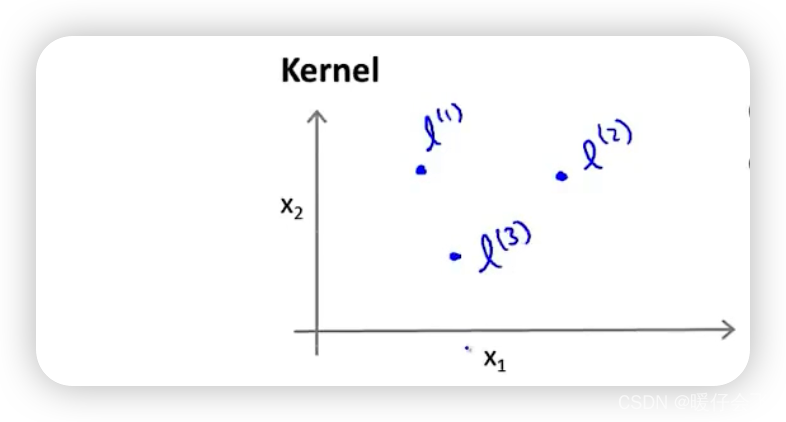
landmark & similarity

• Use to measure the current sample points and some landmark（ Marker points ） Similarity is used to generate $f_1,...,f_n$.

Still use the example mentioned above , For each sample point $x$ Use two features to represent x ⃗ = { x 1 , x 2 } \vec{x}=\{x_1,x_2\} x ={ x1​,x2​}, At this time, we assume that $3$ Different landmarks（ This will be explained in detail later landmarks How it was chosen ）

Next , We measure the samples separately $x$ And these three landmarks Similarity as $f_1,...,f_n$ The process of defining ：

• $f_1=similarity(x,l^{(1)})$
• $f_2=similarity(x,l^{(2)})$
• $f_3=similarity(x,l^{(3)})$
  
  And this $similarity$ We use Gaussian kernel function to define （ I'll explain it in detail later ）
  That is, we use a ：
  $$similarity(x,z)=exp(-\frac{||x-z|{|}^2}{2{\sigma }^2})$$
  therefore , above $f_1,..f_3$ Can be transformed into ：
• $f_1=exp(-\frac{||x-l^{(1)}|{|}^2}{2{\sigma }^2})$
• $f_2=exp(-\frac{||x-l^{(2)}|{|}^2}{2{\sigma }^2})$
• $f_3=exp(-\frac{||x-l^{(3)}|{|}^2}{2{\sigma }^2})$
  Note: $$||x-l^{(1)}|{|}^2={\Sigma }_{i=1}^m(x_i-l_i{)}^2$$ $m$ It's a sample $x$ Number of features used in , Here it is. $x_1,x_2$ Two characteristics, so $m=2$
  
  You can see , Under the definition of this function , If $x$ and $l^{(i)}$ Are very similar , Then the result of the kernel function will be close to $f_i\approx exp(-\frac{0}{2{\sigma }^2})\approx 1$ ; contrary , If $x$ and $l^{(i)}$ Far away , Then the result is close to $0$.
  So we can think of $f_1,...,f_n$ Measured $x$ This sample to these landmark Similar procedures （ Distance metric ）; And these $f_1,...,f_n$ Become a component $x$ This sample is $n$ Features
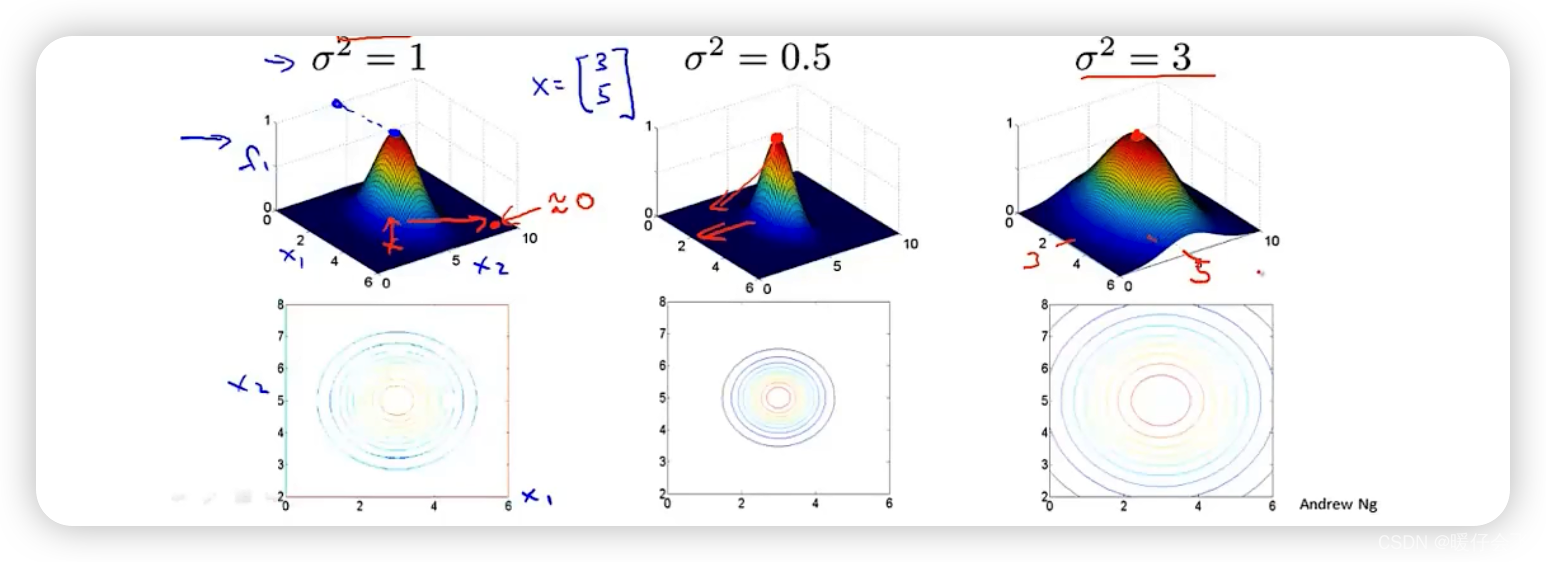
  For ease of understanding , We visualize Gaussian kernel function
  
  As you can see from the picture , When $l^{(1)}$ The closer you are to $x$, Then the result of passing through the Gaussian kernel function is closer to the center of the graph , The closer the value is $1$; contrary , If it is farther away, the value is closer to $0$
  We can also draw a simple conclusion ： Standard deviation of Gaussian kernel function $\sigma$ The size of determines the smoothness of the distribution , For example, choose different $\sigma$ The distribution is different ：
  

How to generate nonlinear boundary

• Let's say we've got through calculation ${\theta }_0,{\theta }_1,...{\theta }_3$, Their values are shown in the figure ：
  
• If there is a sample at this time $x$ In the position in the figure ： distance $l^{(1)}$ Very close , But distance $l^{(2)},l^{(3)}$ Far away , Then we can think that $f_1\approx 1;f_2,f_3\approx 0$ Calculate by bringing in the formula , The final prediction we can get is $>=0$ Of , Positive sample .
  
• If there is another sample at this time $x$, Three $l^{(i)}$ Far away ： According to the same steps, we can calculate that his prediction label is $<0$ Of , Negative samples .
  
• If the sample size is large enough , You'll find that ： The final prediction result of these samples actually depends on all landmarks, The resulting decision boundary will become a nonlinear decision boundary . All samples inside the red boundary will be judged as positive samples , All samples outside the red boundary will be judged as negative samples .
  

How to choose landmarks

• In fact, you may have thought of , We can use all the sample points in this dataset $X=x^{(1)},x^{(2)},...,x^{(n)}$ As these landmarks $$l^{(1)}=x^{(1)},l^{(2)}=x^{(2)},...,l^{(n)}=x^{(n)}$$

• The similarity of samples can be rewritten into the following formula ：

  • $f_1=exp(-\frac{||x-x^{(1)}|{|}^2}{2{\sigma }^2})$
  • $f_2=exp(-\frac{||x-x^{(2)}|{|}^2}{2{\sigma }^2})$
  • $f_3=exp(-\frac{||x-x^{(3)}|{|}^2}{2{\sigma }^2})$
    .
    .
    .
  • $f_n=exp(-\frac{||x-x^{(n)}|{|}^2}{2{\sigma }^2})$

• thus , Every sample $x^{(i)}$ Eigenvector of $\overrightarrow{x^{(i)}}$ By the original { x 1 ( i ) , x 2 ( i ) } \{x^{(i)}_1,x^{(i)}_2\} { x1(i)​,x2(i)​} Turned into f ( i ) ⃗ = { f 1 ( i ) , f 2 ( i ) , . . . , f n ( i ) } \vec{f^{(i)}}=\{f^{(i)}_1, f^{(i)}_2,..., f^{(i)}_n\} f(i) ​={ f1(i)​,f2(i)​,...,fn(i)​}; In fact, we omit the intercept feature here $f_0^{(i)}$, If you want to add it, it's also very simple , f ( i ) ⃗ = { f 0 ( i ) , f 1 ( i ) , f 2 ( i ) , . . . , f n ( i ) } \vec{f^{(i)}}=\{f^{(i)}_0, f^{(i)}_1, f^{(i)}_2,..., f^{(i)}_n\} f(i) ​={ f0(i)​,f1(i)​,f2(i)​,...,fn(i)​}

• The same is about to change , It's with this $n$ Dimension vector （ If you count $f_0$ Namely $n+1$ dimension ） The vector corresponds to $\vec{\theta }={\theta }_0,...,{\theta }_n$

• We finally passed ${\theta }^T\cdot \vec{f}={\theta }_0{f}_0+...+{\theta }_n{f}_n>=0$ To predict a positive sample .

SVM Combined kernel function

• Combine the above , Let's look back SVM The objective function of , For a containing $m$ The data set of 2 samples ：
  $$C{\Sigma }_{i=1}^m{y}_{i}cos{t}_1({\theta }^T{x}^{(i)})+(1-y_i)cos{t}_0({\theta }^T{x}^{(i)})+\frac{1}{2}{\Sigma }_{j=1}^n{\theta }_j^2(1)$$

• We can rewrite this optimization goal as ：
  $$C{\Sigma }_{i=1}^m{y}_{i}cos{t}_1({\theta }^T\cdot \overrightarrow{f^{(i)}})+(1-y_i)cos{t}_0({\theta }^T\cdot \overrightarrow{f^{(i)}})+\frac{1}{2}{\Sigma }_{j=1}^n{\theta }_j^2(2)$$

• That is to put the original $x$ The feature vector is transformed into a new one based on $f$ Eigenvector of ; Now the number of samples is $m$.

• At the same time , Regularized part of $n$ It originally represented a sample $x^{(i)}$ The number of effective features in , Now this quantity can also be replaced by $m$ 了 , Because the number of effective features is the number of samples , So the formula is optimized again to ：

$$C{\Sigma }_{i=1}^m{y}_{i}cos{t}_1({\theta }^T\cdot \overrightarrow{f^{(i)}})+(1-y_i)cos{t}_0({\theta }^T\cdot \overrightarrow{f^{(i)}})+\frac{1}{2}{\Sigma }_{j=1}^m{\theta }_j^2(2)$$

• there $j=1...m$ The feature that cannot contain intercept , That is, this part of regularization , There can only be at most $m$ The item , Because the intercept feature is not included in the optimization of regularization, it cannot be written as $j=0...m$.
• So the regular term can also be written as $${\theta }^T\cdot \theta (ignoring{\theta }_0)$$