当前位置:网站首页>[二叉数] 二叉树的最大深度+N叉树的最大深度
[二叉数] 二叉树的最大深度+N叉树的最大深度
2022-04-23 17:28:00 【Alson_Code】
一、题目描述
原文链接:104. 二叉树的最大深度
具体描述:
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明: 叶子节点是指没有子节点的节点。
示例:
给定二叉树 [3,9,20,null,null,15,7],
3
/ \
9 20
/ \
15 7
返回它的最大深度 3 。
二、思路分析
之前做过一次二叉数的最大深度,其实用的是层次遍历!这次我们用递归的方式!
首先我们理解一句话:前序遍历是深度,后序遍历是深度,深度等于高度!
从这句话可以看出两种解法,一种前序,一种后序!
先说说后序(递归三部曲):
- 确定参数和返回值,返回值就是int类型的深度,参数就是子树+深度
- 终止条件,如果子树为null则返回当前深度
- 单层逻辑就是,遍历左节点,在遍历右节点,比较大小!
再说说前序(递归三部曲):
- 因为先根在左右,所以不能在根就返回值,所以返回值为void,参数还是子树+深度
- 终止条件就是找到左右子树都是空则结束
- 先和当前深度和根比较获取最大值,然后在左右子树递归获取最大值!
三、AC代码
后序遍历:
/** * Definition for a binary tree node. * public class TreeNode { * int val; * TreeNode left; * TreeNode right; * TreeNode() {} * TreeNode(int val) { this.val = val; } * TreeNode(int val, TreeNode left, TreeNode right) { * this.val = val; * this.left = left; * this.right = right; * } * } */
class Solution {
public int maxDepth(TreeNode root) {
return getDepth(root, 0);
}
public int getDepth(TreeNode root, int depth){
if (root == null) return depth;
int leftDepth = getDepth(root.left, depth + 1);// 左
int rightDepth = getDepth(root.right, depth + 1);// 右
return leftDepth > rightDepth ? leftDepth : rightDepth;// 根
}
}
前序遍历:
/** * Definition for a binary tree node. * public class TreeNode { * int val; * TreeNode left; * TreeNode right; * TreeNode() {} * TreeNode(int val) { this.val = val; } * TreeNode(int val, TreeNode left, TreeNode right) { * this.val = val; * this.left = left; * this.right = right; * } * } */
class Solution {
int result = 0;
public int maxDepth(TreeNode root) {
if (root == null) return result;
getDepth(root, 1);
return result;
}
public void getDepth(TreeNode root, int depth){
result = result > depth ? result : depth;// 根
if (root.left != null){
depth++;
getDepth(root.left, depth);
depth--;// 恢复到原来的值,要不然求右子树的话会在左子树的基础上求!
}
if (root.right != null){
depth ++;
getDepth(root.right, depth);
depth--;
}
}
}
四、总结
- 深度=高度,深度就是从根到叶子节点,高度就是从叶子到根!
五、巩固练习
/* // Definition for a Node. class Node { public int val; public List<Node> children; public Node() {} public Node(int _val) { val = _val; } public Node(int _val, List<Node> _children) { val = _val; children = _children; } }; */
class Solution {
public int maxDepth(Node root) {
return getDepth(root, 1);
}
public int getDepth(Node root, int depth){
if (root == null) return 0;
int maxDepth = depth;
for (int i = 0; i < root.children.size(); i++){
int tmpDepth = getDepth(root.children.get(i), depth + 1);
maxDepth = tmpDepth > maxDepth ? tmpDepth : maxDepth;
}
return maxDepth;
}
}
感谢大家的阅读,我是Alson_Code,一个喜欢把简单问题复杂化,把复杂问题简单化的程序猿!
版权声明
本文为[Alson_Code]所创,转载请带上原文链接,感谢
https://blog.csdn.net/weixin_42415173/article/details/124356376
边栏推荐
- [ES6] promise related (event loop, macro / micro task, promise, await / await)
- Abnormal resolution of Xiaomi camera
- El date picker limits the selection range from the current time to two months ago
- Using quartz under. Net core -- job attributes and exceptions of [4] jobs and triggers
- Shell-sort命令的使用
- Clickhouse table engine
- [related to zhengheyuan cutting tools]
- [difference between Oracle and MySQL]
- Document operation II (5000 word summary)
- Lock lock
猜你喜欢
Advantages and disadvantages of several note taking software
Shell script -- shell programming specification and variables
Milvus 2.0 質量保障系統詳解

Signalr can actively send data from the server to the client
Bottom processing of stack memory in browser

XTask与Kotlin Coroutine的使用对比

Milvus 2.0 détails du système d'assurance de la qualité
![[PROJECT] small hat takeout (8)](/img/54/0187eeb637f4dcd4ad3969b00e2b77.png)
[PROJECT] small hat takeout (8)
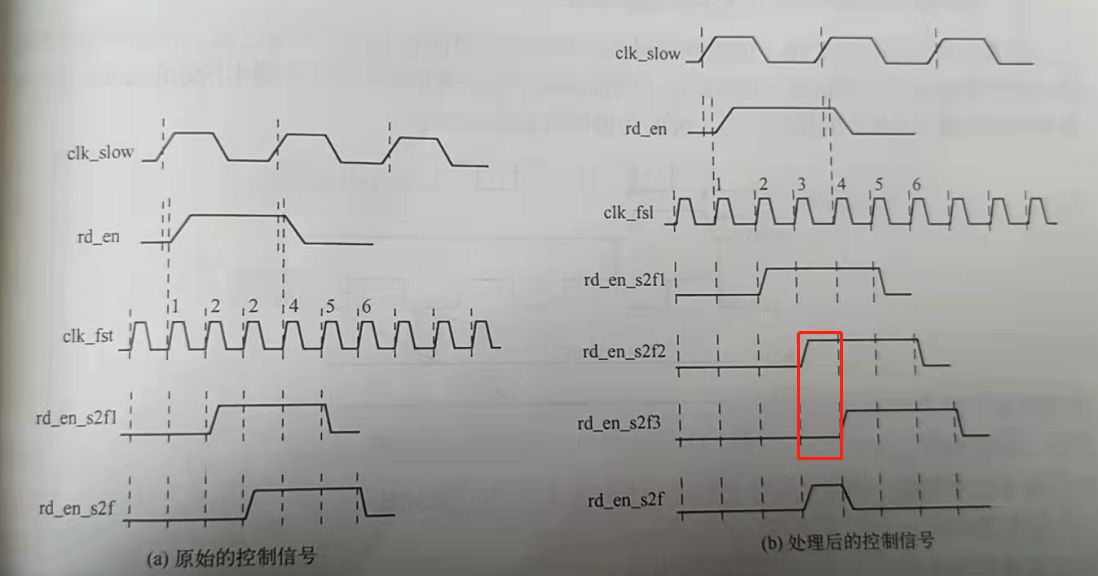
快时钟同步慢时钟域下的异步控制信号slow clk to fast clk
Qt 修改UI没有生效
随机推荐
文件操作《二》(5000字总结篇)
Devexpress GridView add select all columns
Freecodecamp ---- budget & category exercise
Self use learning notes - connectingstring configuration
ASP. Net core configuration options (Part 2)
Preliminary understanding of promse
Handwritten event publish subscribe framework
.Net Core3. 1 use razorengine NETCORE production entity generator (MVC web version)
Net standard
Understanding of RPC core concepts
1-1 NodeJS
Advantages and disadvantages of several note taking software
Further study of data visualization
Websocket (basic)
Aiot industrial technology panoramic structure - Digital Architecture Design (8)
Entity Framework core captures database changes
Bottom processing of stack memory in browser
matlab如何绘制已知公式的曲线图,Excel怎么绘制函数曲线图像?
Input file upload
ClickHouse-表引擎