当前位置:网站首页>机器学习——逻辑回归
机器学习——逻辑回归
2022-04-23 15:08:00 【請叫我做雷锋】
一、二项逻辑回归
1.二项逻辑回归是一个功能,最终输出介于0到1之间的值,为了解决类似于“成功或者失败”,“有或无"这种”非是即否"的问题。
2.逻辑回归是一个把线性回归模型映射为概率的模型,即把实数空间的输出[-∞,+∞]映射到(0,1),从而获取概率。(个人理解:回归的含义——用观察使得认知接近真值的过程,回归本源。)
3.通过画图的方式来直观认识这种映射,我们首先定义一个二元线性回归模型:
y ^ = θ 1 x 1 + θ 2 x 2 + b i a s , 其 中 y ^ ∈ ( − ∞ , + ∞ ) \hat{y}=\theta_1x_1+\theta_2x_2+bias, 其中\hat{y}∈(-∞,+∞) y^=θ1x1+θ2x2+bias,其中y^∈(−∞,+∞)
线性回归图:
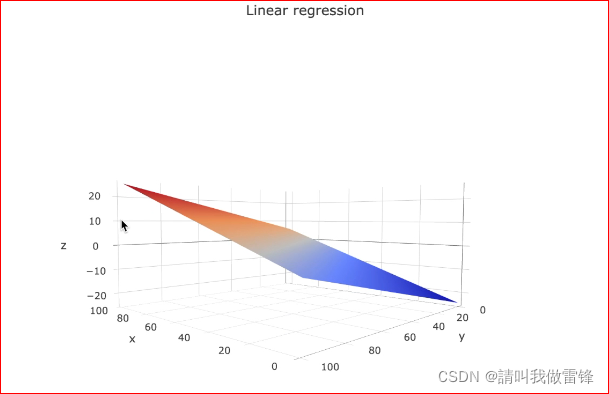
逻辑回归图:
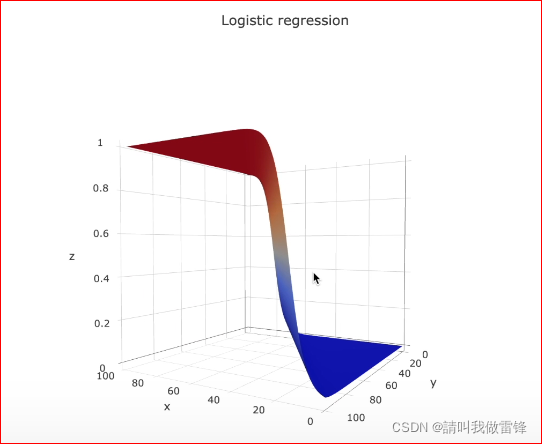
二、probability和odds的定义
1.probability指的是 发生的次数/总次数 ,以抛硬币为例:

p的取值范围为[0,+∞)
2.odds则是一种比率,是指某事件发生的可能性(概率)与不发生的可能性(概率)之比。即 发生的次数/没有发生的次数 ,以抛硬币为例:

odds的取值范围为[0,+∞)
3.回顾伯努利分布:如果X是伯努利分布中的随机变量,X的取值为{0,1},非0即1,如抛硬币的正反面:
则:P(X=1)=p,P(X=0)=1-p
代入odds:
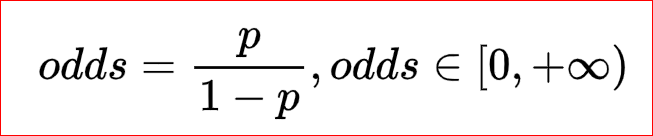
三、logit函数和sigmoid函数及他们的特性:
1.Odds的对数称之为Logit,也写作log-it。
2.我们对odds取log,扩展odds的取值范围到实数空间[-∞,+∞],这就是logit函数:
l o g i t ( p ) = l o g e ( o d d s ) = l o g e ( p 1 − p ) , p ∈ ( 0 , 1 ) , l o g i t ( p ) ∈ ( − ∞ , + ∞ ) logit(p)=log_e(odds)=log_e(\frac{p}{1-p}),p∈(0,1),logit(p)∈(-∞,+∞) logit(p)=loge(odds)=loge(1−pp),p∈(0,1),logit(p)∈(−∞,+∞)
3.我们可以使用线性回归模型来表示logit§,因为线性回归模型和logit函数的输出有着同样的取值范围:
例如: l o g i t ( p ) = θ 1 x 1 + θ 2 x 2 + b i a s logit(p)=\theta_1x_1+\theta_2x_2+bias logit(p)=θ1x1+θ2x2+bias
以下是logit§的函数图像,注意p∈(0,1),当p=0或者p=1时,logit属于未定义。
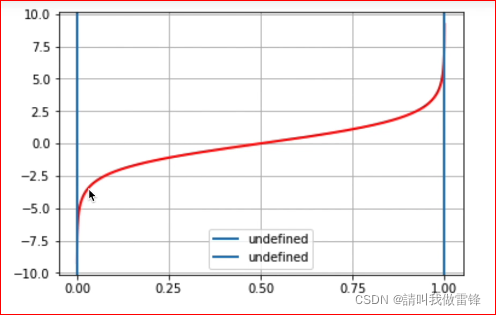
由 l o g i t ( p ) = θ 1 x 1 + θ 2 x 2 + b i a s logit(p)=\theta_1x_1+\theta_2x_2+bias logit(p)=θ1x1+θ2x2+bias
得
l o g ( p 1 − p ) = θ 1 x 1 + θ 2 x 2 + b i a s log(\frac{p}{1-p} )=\theta_1x_1+\theta_2x_2+bias log(1−pp)=θ1x1+θ2x2+bias
注:可能有人会产生误解,不理解如何转换,logit§表示的是与参数p相关的对数函数,在这里
logit( p )=log(p/(1-p))。
设 z = θ 1 x 1 + θ 2 x 2 + b i a s z=\theta_1x_1+\theta_2x_2+bias z=θ1x1+θ2x2+bias
得 l o g ( p 1 − p ) = z log(\frac{p}{1-p} )=z log(1−pp)=z
等式两边取以e为敌的指数函数:
p 1 − p = e z \frac{p}{1-p}=e^{z} 1−pp=ez
p = e z ( 1 − p ) = e z − e z p p=e^{z}(1-p)=e^{z}-e^{z}p p=ez(1−p)=ez−ezp
p ( 1 + e z ) = e z p(1+e^z)=e^z p(1+ez)=ez
p = e z ( 1 + e z ) p=\frac{e^z}{(1+e^z)} p=(1+ez)ez
分子分母同时除以 e z e^z ez,得
p = 1 ( 1 + e − z ) , p ∈ ( 0 , 1 ) p=\frac{1}{(1+e^{-z})} ,p∈(0,1) p=(1+e−z)1,p∈(0,1)
经过上面的推导,我们得出了sigmoid函数,最终把线性回归模型输出的实数空间取值映射成为概率了。
s i g m o i d ( z ) = 1 1 + e − z , p ∈ ( 0 , 1 ) sigmoid(z)=\frac{1}{1+e^{-z}} ,p∈(0,1) sigmoid(z)=1+e−z1,p∈(0,1)
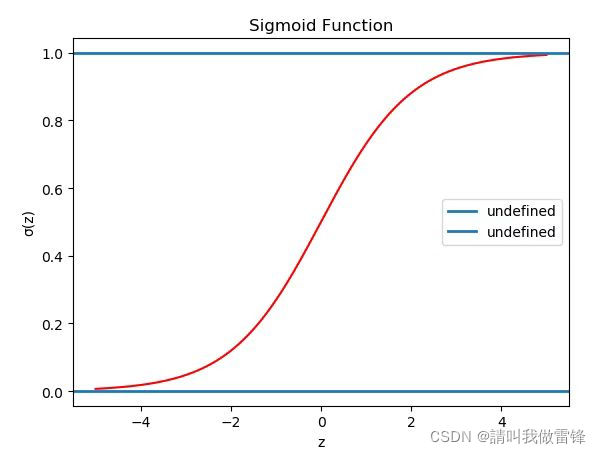
下面是sigmoid的函数图像,注意sigmoid(z)的取值范围
四、最大似然估计
1.引入假设函数 h θ ( X ) h_\theta(X) hθ(X),设 θ T X \theta^TX θTX为线性回归模型:
θ T X \theta^TX θTX中, θ T \theta^T θT和X均为列向量,例如:
θ T = [ b i a s θ 1 θ 2 ] \theta^T=\begin{bmatrix} bias & \theta_1 &\theta_2 \end{bmatrix} θT=[biasθ1θ2]
X = [ 1 x 1 x 2 ] X=\begin{bmatrix} 1 \\ x_1 \\ x_2 \end{bmatrix} X=⎣⎡1x1x2⎦⎤
求矩阵点积,得出:
θ T X = b i a s ∗ 1 + θ 1 ∗ x 1 + θ 2 ∗ x 2 = θ 1 x 1 + θ 2 ∗ x 2 + b i a s \theta^TX=bias*1+\theta_1*x_1+\theta_2*x_2=\theta_1x_1+\theta_2*x_2+bias θTX=bias∗1+θ1∗x1+θ2∗x2=θ1x1+θ2∗x2+bias
设 θ T X = z \theta^TX=z θTX=z,则有假设函数:
h θ ( X ) = 1 1 + e − z = P ( Y = 1 ∣ X ; θ ) h_\theta (X)=\frac{1}{1+e^{-z}} =P(Y=1|X;\theta ) hθ(X)=1+e−z1=P(Y=1∣X;θ)
上式表示的是在条件X和 θ \theta θ下Y=1的概率;
P ( Y = 1 ∣ X ; θ ) = 1 − h θ ( X ) P(Y=1|X;\theta )=1-h_\theta(X) P(Y=1∣X;θ)=1−hθ(X)
上式表示的是在条件X和 θ \theta θ下Y=1=0的概率。
2.回顾伯努利分布
f ( k ; p ) { p , i f k = 1 q = 1 − p , i f k = 0 f(k;p)\left\{\begin{matrix} p, &if&k=1 \\ q=1-p, &if&k=0 \end{matrix}\right. f(k;p){
p,q=1−p,ififk=1k=0
或者 f ( k ; p ) = p k ( 1 − p ) 1 − k f(k;p)=p^k(1-p)^{1-k} f(k;p)=pk(1−p)1−k,for k∈{0,1}。注意f(k;p)表示的是k为0或1的概率,也就是P(k)
3.最大似然估计得目的是找到一个最符合数据的概率分布。
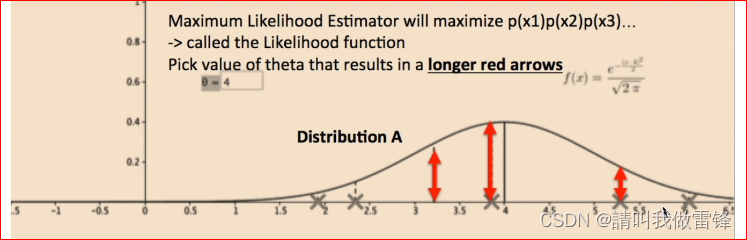
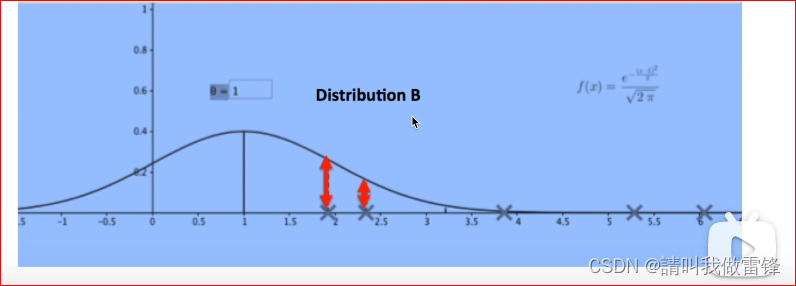
例如下图中的XX指的是数据点,图中所有红色箭头长度的乘积就是似然函数的输出,显然,上半图的分布似然函数要比下半图的大,所以上半图的分布更符合数据,而最大似然估计就是找到一个最符合当前数据的分布。
4.定义似然函数
L ( θ ∣ x ) = P ( Y ∣ X ; θ ) = ∏ i m P ( y i ∣ x i ; θ ) = ∏ i m h θ ( x i ) y i ( 1 − h θ ( x i ) ) ( 1 − y i ) L(\theta|x)=P(Y|X;\theta )=\prod_{i}^{m} P(y_i|x_i;\theta )=\prod_{i}^{m} h_\theta(x_i)^{y_i}(1-h_\theta(x_i))^{(1-{y_i})} L(θ∣x)=P(Y∣X;θ)=i∏mP(yi∣xi;θ)=i∏mhθ(xi)yi(1−hθ(xi))(1−yi),
其中i为每个数据样本,共有m个数据样本,最大似然估计的目的是让上式的“从输出值”尽可能大;对上式取log,以方便计算,因为log可以把乘积转换为加法,而且不影响我们的优化目标:
L ( θ ∣ x ) = l o g ( P ( Y ∣ X ; θ ) ) = ∑ i = 1 m y i l o g ( h θ ( x i ) ) + ( 1 − y i ) l o g ( 1 − h θ ( x i ) ) L(\theta|x)=log(P(Y|X;\theta ))=\sum_{i=1}^{m} y_ilog(h_\theta (x_i))+(1-y_i)log(1-h_\theta (x_i)) L(θ∣x)=log(P(Y∣X;θ))=i=1∑myilog(hθ(xi))+(1−yi)log(1−hθ(xi))
我们只要在式子前面加一个负号,即可把求最大转化为求最小,设 h θ ( X ) = Y ^ h_\theta (X)=\hat{Y} hθ(X)=Y^,得出损失函数 J ( θ ) J(\theta) J(θ),我们只要最小化这个函数,就能通过求导来得到我们想要的 θ \theta θ:
J ( θ ) = − ∑ i m Y l o g ( Y ^ ) − ( 1 − Y ) l o g ( 1 − Y ^ ) J(\theta)=-\sum_{i}^{m} Ylog(\hat{Y})-(1-Y)log(1-\hat{Y}) J(θ)=−i∑mYlog(Y^)−(1−Y)log(1−Y^)
版权声明
本文为[請叫我做雷锋]所创,转载请带上原文链接,感谢
https://blog.csdn.net/weixin_44646187/article/details/124354252
边栏推荐
- Llvm - generate addition
- LeetCode165-比较版本号-双指针-字符串
- When splicing HQL, the new field does not appear in the construction method
- Detailed comparison between asemi three-phase rectifier bridge and single-phase rectifier bridge
- UML learning_ Day2
- Comment eolink facilite le télétravail
- Openfaas practice 4: template operation
- 如何设计一个良好的API接口?
- SSH connects to the remote host through the springboard machine
- adobe illustrator 菜單中英文對照
猜你喜欢
Differential privacy (background)

LeetCode151-颠倒字符串中的单词-字符串-模拟
![Detailed explanation of C language knowledge points - data types and variables [2] - integer variables and constants [1]](/img/d4/9ee62772b42fa77dfd68a41bde1371.png)
Detailed explanation of C language knowledge points - data types and variables [2] - integer variables and constants [1]
Kubernetes详解(十一)——标签与标签选择器
LeetCode149-直线上最多的点数-数学-哈希表
For 22 years, you didn't know the file contained vulnerabilities?

大文件如何快速上传?
Kubernetes详解(九)——资源配置清单创建Pod实战

My raspberry PI zero 2W toss notes to record some problems and solutions
Explain TCP's three handshakes in detail
随机推荐
Ffmpeg installation error: NASM / yasm not found or too old Use --disable-x86asm for a clipped build
让阿里P8都为之着迷的分布式核心原理解析到底讲了啥?看完我惊了
Basic operation of circular queue (Experiment)
Mysql连接查询详解
Progress in the treatment of depression
SQLSERVER事物与锁的问题
Subnet division of flannel principle
牛客网数据库SQL实战详细剖析(26-30)
win10 任务栏通知区图标不见了
Five data types of redis
大文件如何快速上传?
填充每个节点的下一个右侧节点指针 II [经典层次遍历 | 视为链表 ]
【thymeleaf】处理空值和使用安全操作符
Fill in the next right node pointer II of each node [classical hierarchy traversal | regarded as linked list]
js——實現點擊複制功能
How to design a good API interface?
How to use OCR in 5 minutes
thinkphp5+数据大屏展示效果
Will golang share data with fragment append
HJ31 单词倒排